Solve a small-molecule structure
The following is based on the experience of a protein crystallographer who one day obtained a small-molecule dataset and managed to solve and refine it without prior knowledge what the crystallized substance was, and without experience in small-molecule crystallography. It was a very rewarding experience (see the figure at the bottom) which is why it's written up here.
This writeup is only meant for the protein crystallographer who occasionally has to use existing tools on a small-molecule dataset. To understand things more thoroughly, one has to read http://shelx.uni-ac.gwdg.de/SHELX/shelx.pdf . There are lots of tutorials available from George Sheldrick's website, but also from others, e.g. [1].
Maybe it should also be stated that this was a simple case, without e.g. twinning or disorder! Furthermore, the hand of the structure was not an issue.
Reduce the data with your favourite data processing software
I use XDS. The decision about the spacegroup has to be postponed, but it surely helps if the correct Laue group is employed during scaling. In the case considered here, the CORRECT step suggested P222 (XDS really only should suggest "222 point symmetry" because CORRECT does not look at systematic absences at this point).
Determine the spacegroup
There are two ways to determine the spacegroup:
These two possibilities also differ in the way how to obtain a file suitable for input to the SHELX program.
If there are different spacegroup possibilities then (downstream, in structure solution and refinement) we need to try all of them in turn, until we hit one that refines really satisfactorily (R-factor below, say, 5%) and gives a structure that makes sense.
use XPREP to find possible spacegroups
First, convert the reflection file to HKLF 4 format (intensities!). The HKLF 4 format is what the SHELX programs read. I used XDSCONV and the following XDSCONV.INP:
SPACE_GROUP_NUMBER= 1 UNIT_CELL_CONSTANTS= 14.433 28.704 8.488 90.000 90.000 90.000 INPUT_FILE=XDS_ASCII.HKL OUTPUT_FILE=temp.hkl
It is important that - to preserve the full information about systematic absences, for use in XPREP - XDSCONV runs in spacegroup 1. This does not necessarily mean that CORRECT also has to run in spacegroup 1, because XDS_ASCII.HKL has all observations no matter in which spacegroup the CORRECT step runs. As long as the spacegroup used in the CORRECT step is primitive, this works nicely. But if some re-indexing between CORRECT's spacegroup and P1 is necessary (like in I, F, C, R) then it is probably safest to rather just run CORRECT in P1.
Run "xprep temp.hkl", answer the question concerning the cell axes, and then hit <Enter> several (about 6) times until the program suggests a list of spacegroups - this list is going to be important. It may help to observe whether the data are centrosymmetric or not, from the line: Mean |E*E-1| = 0.939 [expected .968 centrosym and .736 non-centrosym]. Fortunately, this time there's only one spacegroup consistent with the data:
SPACE GROUP DETERMINATION
Lattice exceptions: P A B C I F Obv Rev All
N (total) = 0 28832 28824 28788 28823 43222 38376 38344 57564
N (int>3sigma) = 0 17961 18421 18158 17862 27270 24715 24627 36959
Mean intensity = 0.0 22.7 23.7 24.8 23.4 23.7 24.7 24.8 24.8
Mean int/sigma = 0.0 9.6 10.0 9.9 9.6 9.8 10.0 10.0 10.0
Crystal system O and Lattice type P selected
Mean |E*E-1| = 0.939 [expected .968 centrosym and .736 non-centrosym]
Chiral flag NOT set
Systematic absence exceptions:
b-- c-- n-- 21-- -c- -a- -n- -21- --a --b --n --21
N 1884 1884 1892 7 988 1014 992 28 545 541 534 72
N I>3s 706 706 0 0 304 0 304 0 0 203 203 0
<I> 25.2 25.2 0.5 0.0 18.2 0.4 18.1 0.4 0.4 25.0 25.4 0.4
<I/s> 7.3 7.3 0.5 0.2 6.6 0.5 6.6 0.5 0.4 7.4 7.6 0.4
Identical indices and Friedel opposites combined before calculating R(sym)
Option Space Group No. Type Axes CSD R(sym) N(eq) Syst. Abs. CFOM
[A] Pccn # 56 centro 3 196 0.023 10123 0.5 / 6.6 2.23
Option [A] chosen
After that, say "c" for "define unit-cell CONTENTS", and input a reasonable number of carbon atoms (I used C20). Get out of this menu with "E". Then, choose "f" for "set up shelxtl FILES". Then, answer the question "XM/SHELXD (M) or XS/SHELXS (S) format [S]:" with "m" since we're going to use shelxd for solving the structure. Answer the question about the name (I used the spacegroup number as I knew I would have to test several possibilities). Finally, "q"uit the program. This writes 56.ins :
TITL 56 in Pccn CELL 0.71073 14.4330 28.7040 8.4880 90.000 90.000 90.000 ZERR 11.00 0.0029 0.0057 0.0017 0.000 0.000 0.000 LATT 1 SYMM 0.5-X, 0.5-Y, Z SYMM -X, 0.5+Y, 0.5-Z SYMM 0.5+X, -Y, 0.5-Z SFAC C UNIT 220 FIND 16 PLOP 22 27 31 MIND 1.0 -0.1 NTRY 1000 HKLF 4 END
use POINTLESS to find possible spacegroups
Unless the spacegroup number in XDS_ASCII.HKL already indicates this, pointless needs to be told that the spacegroup may not be restricted to those 65 which occur for crystals from macromolecules:
echo CHIRALITY NONCHIRAL | pointless xdsin XDS_ASCII.HKL
gives
Zone Number PeakHeight SD Probability ReflectionCondition
Zones for Laue group P m m m
1 screw axis 2(1) [a] 11 0.990 0.135 *** 0.972 h00: h=2n
2 screw axis 2(1) [b] 59 1.000 0.097 *** 0.986 0k0: k=2n
3 screw axis 2(1) [c] 131 0.997 0.062 *** 0.994 00l: l=2n
4 glide plane b(a) 3754 0.012 0.050 0.000 0kl: k=2n
5 glide plane c(a) 3754 0.013 0.050 0.000 0kl: l=2n
6 glide plane n(a) 3754 0.951 0.061 *** 0.988 0kl: k+l=2n
7 glide plane a(b) 1961 0.953 0.050 *** 0.990 h0l: h=2n
8 glide plane c(b) 1961 0.104 0.056 0.004 h0l: l=2n
9 glide plane n(b) 1961 0.100 0.056 0.004 h0l: h+l=2n
10 glide plane a(c) 1074 0.960 0.058 *** 0.991 hk0: h=2n
11 glide plane b(c) 1074 0.080 0.058 0.003 hk0: k=2n
12 glide plane n(c) 1074 0.072 0.050 0.002 hk0: h+k=2n
<!--SUMMARY_END-->
Possible spacegroups:
--------------------
Indistinguishable space groups are grouped together on successive lines
'Reindex' is the operator to convert from the input hklin frame to the standard spacegroup frame.
'SysAbsProb' is an estimate of the probability of the space group based on
the observed systematic absences.
'Conditions' are the reflection conditions (absences)
'TotProb' is a total probability estimate (unnormalised) including the probability
of the crystal being centrosymmetric from the <|E^2-1|> statistic.
Chiral space groups are marked '*' and centrosymmetric ones 'O'
Spacegroup TotProb SysAbsProb Reindex Conditions
<P n a a> ( 56) O 0.823 0.911 h00: h=2n, 0k0: k=2n, 00l: l=2n, 0kl: k+l=2n, h0l: h=2n, hk0: h=2n (zones 1,2,3,6,7,10)
---------------------------------------------------------------
Selecting space group P n a a as there is a single space group with the highest score
The spacegroup that was used for CORRECT does not matter. The next step then is to generate a HKLF 4 file, using XDSCONV:
SPACE_GROUP_NUMBER= 56 UNIT_CELL_CONSTANTS= 14.433 28.704 8.488 90.000 90.000 90.000 INPUT_FILE=XDS_ASCII.HKL OUTPUT_FILE=56.hkl
Please note that the file 56.ins has to be set up manually in this case (just take the 56.ins from above, and adjust the symops and cell parameters). The numbers after "FIND" and "PLOP" should probably be adjusted in proportion to the expected number of atoms in the asymmetric unit.
Solve the structure with SHELXD
Just run "shelxd 56". You may interrupt it with Ctrl-C once it has found a good solution, as suggested by
Try 11:20 Peaks 99 92 87 87 87 83 77 73 71 70 68 68 64 64 64 63 62 62 61 60 R = 0.294, Min.fun. = 0.747, <cos> = 0.491, Ra = 0.235 Try 11, CC All/Weak 59.81 / 46.01, best 59.81 / 46.01, best final CC 0.00 Peaklist optimization cycle 1 CC = 77.51 % BG = 0.322 for 22 atoms Peaks: 99 90 87 85 82 77 75 74 66 64 64 64 63 63 62 57 39 39 36 36 33 31 Fragments: 17 5 Peaklist optimization cycle 2 CC = 88.80 % BG = 0.225 for 25 atoms Peaks: 99 95 89 88 87 84 82 79 78 78 77 76 75 75 74 73 73 71 71 69 67 65 40 Fragments: 25 Peaklist optimization cycle 3 CC = 88.85 % BG = 0.223 for 25 atoms Peaks: 99 96 89 87 86 86 82 79 79 76 76 75 75 75 73 73 72 71 69 69 67 65 63 Fragments: 25
This solution obviously fulfills the requirement "When the final correlation coefficient CC (after PLOP) for an atomic resolution ab initio run of SHELXD is 65% or greater, the structure is almost certainly solved." in http://shelx.uni-ac.gwdg.de/SHELX/shelxdec/shelx-de.pdf .
The resulting 56.res is:
REM TRY 23 FINAL CC 88.85 TIME 3 SECS REM Fragments: 25 REM TITL 56 in Pccn CELL 0.71073 14.4330 28.7040 8.4880 90.000 90.000 90.000 ZERR 11.00 0.0029 0.0057 0.0017 0.000 0.000 0.000 LATT 1 SYMM 0.5-X, 0.5-Y, Z SYMM -X, 0.5+Y, 0.5-Z SYMM 0.5+X, -Y, 0.5-Z SFAC C UNIT 220 C001 1 0.45835 0.41566 0.09083 11.00000 0.1 99.00 C002 1 0.36894 0.55007 -0.58932 11.00000 0.1 95.84 C003 1 0.52129 0.72099 -0.95623 11.00000 0.1 89.35 C004 1 0.67521 0.30725 0.04587 11.00000 0.1 87.55 C005 1 0.40328 0.54911 -0.45947 11.00000 0.1 85.96 ... C021 1 0.60567 0.70055 -0.97749 11.00000 0.1 66.94 C022 1 0.49503 0.62079 -0.48787 11.00000 0.1 64.91 C023 1 0.60066 0.62034 -0.48599 11.00000 0.1 63.62 C024 1 0.63251 0.26331 0.06189 11.00000 0.1 63.01 C025 1 0.47217 0.73227 -1.09548 11.00000 0.1 61.79 HKLF 4 END
Refine using SHELXL
Copy 56.res to 56.ins. Insert
ACTA LIST 6 L.S. 10
after the UNIT 220 instruction, and run "shelxl 56". This gives a first refined model, and its electron density map, plus the relevant statistics.
general idea of refining a structure
Starting from a rough guess of the number of atoms, we adjust the model, guided by the refinement results. This is an iterative process, in which we repeatedly edit 56.res to reflect our change of conception of the structure, replace 56.ins with it, and run SHELXL again.
assigning chemical types
Since we know that there's not only carbon atoms, but likely also N, O and H, we modify 56.ins to have
SFAC C N O H UNIT 200 100 100 40
(the actual numbers after UNIT can be taken from the .lst file of SHELXL, they don't seem to matter much.)
We tell SHELXL the chemical identity by putting a 1 for a C, a 2 for a N, a 3 for an O, and a 4 for a H - the number is just the order of the atom in the SFAC line.
The chemical identity of an atom can be found from geometric parameters, and its electron density. The electron density can be displayed e.g. in coot, by loading the 56.fcf file written by SHELXL. Geometric parameters (in particular distances) are listed in the 56.lst file. Typical bond distances of C-C, C=C, C-O, C=O, C-N and X-H are about 1.54, 1.34, 1.43, 1.24, 1.47 and 1.0 A, respectively.
As a proxy to electron density we can use the refined ADPs. Atoms initially called "C", but with very low U values after refinement, are most likely O or N atoms.
For the H atoms, we just cut-and-paste the atoms from the bottom of the .res file into those lines where the other atoms are, if the distances to existing (heavy) atoms are close to 1 A.
Finishing the structure
Finally we switch to anisotropic refinement by putting an
ANIS
line into 56.ins . More info about refinement options is in the SHELXL article!
Resolution
To quote George Sheldrick:: SHELXL "prints R values for all data and for I>2sig(I) [F>4sig(F)]. The user can of course improve these by cutting back the resolution but if he or she oversteps 0.84A he/she will be caught by the CIF police. This works like a radar trap so weak datasets are usually truncated to 0.84A whether or not there are significant data to that resolution. It is always instructive to compare the R-values for all data and I>2sig(I); if the former is substantially larger, a lot of noisy outer data have been included."
Electron density
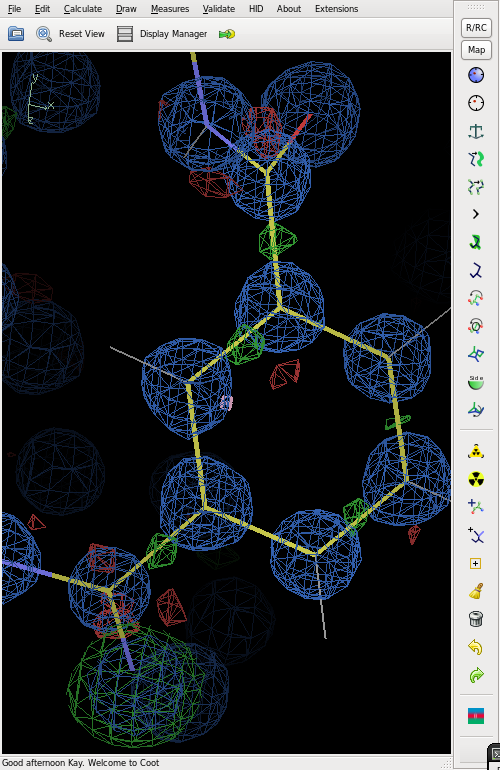
The figure shows the final electron density (blue), but with an O atom refined as N. This gives strong positive (green) difference electron density.
The difference map also shows distinct bonding electron density on most of the bonds.