MINIMUM ZETA: Difference between revisions
mNo edit summary |
m update links |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
As always, the authoritative documentation is at http:// | As always, the authoritative documentation is at http://xds.mpimf-heidelberg.mpg.de/html_doc/xds_parameters.html#MINIMUM_ZETA= ! | ||
== What is MINIMUM_ZETA? == | == What is MINIMUM_ZETA? == | ||
MINIMUM_ZETA is a parameter determining how close reflections may be to the 'blind region' of reciprocal space to still be integrated. On the detector, the blind region consists of two cones starting at the direct beam position, and extending along the spindle, to both directions. | MINIMUM_ZETA is a parameter determining how close reflections may be to the 'blind region' of reciprocal space to still be integrated. On the detector, the blind region consists of two cones starting at the direct beam position, and extending along the spindle, to both directions. | ||
== How could I check if a low value of MINIMUM_ZETA is beneficial for my data reduction? == | == How could I check if a low value of MINIMUM_ZETA is beneficial for my data reduction? == | ||
| Line 19: | Line 17: | ||
We collected data at the SLS, beamline X06SA, on a MarCCD 225 detector. Below, I show the final output of CORRECT.LP and a mapping of R-factors on the surface of the detector (file rf.pck produced by XDSSTAT). | We collected data at the SLS, beamline X06SA, on a MarCCD 225 detector. Below, I show the final output of CORRECT.LP and a mapping of R-factors on the surface of the detector (file rf.pck produced by XDSSTAT). | ||
Using the default value of MINIMUM_ZETA= 0.15, one obtains in CORRECT.LP: | Using the former default value of MINIMUM_ZETA= 0.15, one obtains in CORRECT.LP (this is from a 2010 version of XDS): | ||
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION | SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION | ||
| Line 81: | Line 79: | ||
[[Image:ms688-frame.png]] | [[Image:ms688-frame.png]] | ||
From looking at rf.pck of many datasets, it is my experience that at the SLS (X06SA | From looking at rf.pck of many datasets, it is my experience that at the SLS (beamline X06SA), the R-factors along the spindle are better than perpendicular to it, which is quite surprising (and should be investigated). Therefore it is clear that in particular for these data it is a good thing to decrease MINIMUM_ZETA because accurately measured reflections are added to the data set. | ||
Latest revision as of 11:24, 22 October 2019
As always, the authoritative documentation is at http://xds.mpimf-heidelberg.mpg.de/html_doc/xds_parameters.html#MINIMUM_ZETA= !
What is MINIMUM_ZETA?
MINIMUM_ZETA is a parameter determining how close reflections may be to the 'blind region' of reciprocal space to still be integrated. On the detector, the blind region consists of two cones starting at the direct beam position, and extending along the spindle, to both directions.
How could I check if a low value of MINIMUM_ZETA is beneficial for my data reduction?
It does not hurt to use a low value of MINIMUM_ZETA (e.g. 0.03) in INTEGRATE, because in CORRECT you may still choose higher values (i.e. you don't then have to re-run INTEGRATE if you want to test a different value).
Then, run CORRECT with the low values and with higher values and compare the resulting completeness and R-factors.
For a finer evaluation, you might want to inspect with VIEW the file 'rf.pck' of XDSSTAT .
An example
We collected data at the SLS, beamline X06SA, on a MarCCD 225 detector. Below, I show the final output of CORRECT.LP and a mapping of R-factors on the surface of the detector (file rf.pck produced by XDSSTAT).
Using the former default value of MINIMUM_ZETA= 0.15, one obtains in CORRECT.LP (this is from a 2010 version of XDS):
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
6.78 76993 19828 19942 99.4% 3.5% 4.8% 76973 23.88 4.1% 3.0% -10% 0.599 9080
4.81 138283 35547 35595 99.9% 7.5% 7.5% 138249 15.56 8.7% 6.8% -4% 0.792 16881
3.94 177582 45838 45943 99.8% 8.7% 8.3% 177446 13.94 10.1% 8.4% -2% 0.825 21918
3.41 203352 54169 54469 99.4% 16.9% 16.0% 203075 7.93 19.8% 19.6% 9% 0.898 25847
3.05 228865 61477 61637 99.7% 33.9% 34.4% 228019 4.08 39.6% 43.5% 1% 0.805 29056
2.79 240279 67660 68124 99.3% 58.4% 61.1% 237748 2.33 68.8% 77.3% 2% 0.770 30609
2.58 241037 72697 74116 98.1% 99.3% 100.1% 235667 1.42 118.4% 128.7% 6% 0.803 30621
2.42 237676 77079 79650 96.8% 121.2% 129.7% 228955 0.98 145.8% 170.6% 2% 0.722 30204
2.28 173189 71762 84696 84.7% 135.7% 148.8% 156159 0.71 170.1% 220.0% 2% 0.708 21582
total 1717256 506057 524172 96.5% 18.8% 19.3% 1682291 5.40 22.2% 43.2% 2% 0.782 215798
and rf.pck generated by XDSSTAT looks like:
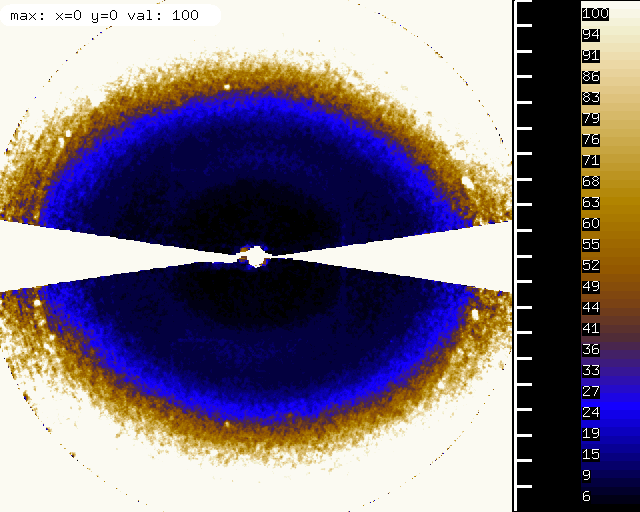
With MIMUM_ZETA=0.1 the R-factors and completeness stays the same, but a closer look (not unexpectedly) reveals that the total number of observed reflections rises:
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
6.78 77465 19824 19942 99.4% 3.5% 4.8% 77445 23.89 4.1% 3.0% -7% 0.600 9078
4.81 139162 35560 35598 99.9% 7.5% 7.5% 139162 15.62 8.7% 6.7% -4% 0.794 16926
3.94 178677 45842 45940 99.8% 8.7% 8.3% 178652 14.00 10.1% 8.3% -2% 0.829 22029
3.41 204689 54186 54467 99.5% 16.8% 15.9% 204526 7.99 19.6% 19.6% 9% 0.899 25971
3.05 230193 61486 61641 99.7% 33.7% 34.2% 229403 4.13 39.4% 43.5% 1% 0.807 29119
2.79 241535 67657 68124 99.3% 58.1% 60.7% 239037 2.36 68.3% 77.2% 2% 0.771 30638
2.58 242127 72709 74118 98.1% 98.2% 99.1% 236782 1.44 117.0% 128.0% 6% 0.800 30656
2.42 238367 77083 79650 96.8% 120.9% 129.4% 229693 0.99 145.4% 171.2% 2% 0.723 30257
2.28 173359 71759 84698 84.7% 135.4% 148.5% 156346 0.71 169.7% 219.9% 2% 0.705 21596
total 1725574 506106 524178 96.6% 18.6% 19.2% 1691046 5.43 22.0% 43.1% 2% 0.783 216270
obviously the cones along the spindle are narrower:
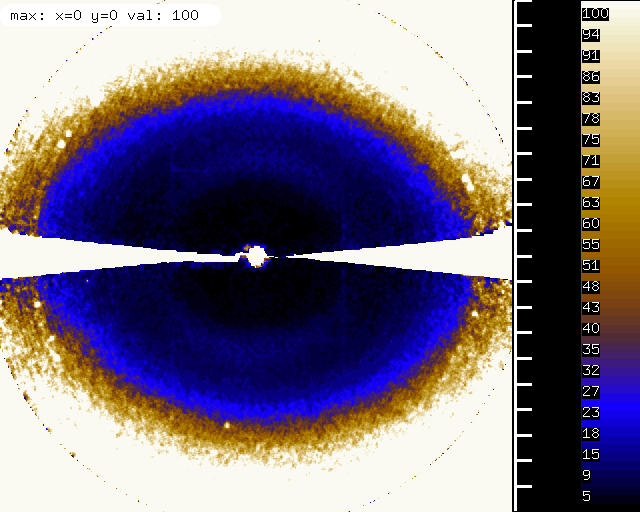
Finally, with MINIMUM_ZETA=0.01 the number of observed reflections gets even higher:
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
6.78 77625 19826 19942 99.4% 3.6% 4.8% 77605 23.77 4.1% 2.9% -11% 0.596 9077
4.81 139571 35562 35598 99.9% 7.5% 7.5% 139571 15.60 8.7% 6.7% -4% 0.794 16927
3.94 179276 45840 45942 99.8% 8.7% 8.3% 179269 14.00 10.1% 8.3% -2% 0.834 22034
3.41 205281 54202 54465 99.5% 16.7% 15.9% 205131 8.01 19.6% 19.5% 10% 0.903 25999
3.05 230671 61495 61643 99.8% 33.5% 34.0% 229887 4.14 39.2% 43.6% 1% 0.806 29133
2.79 241775 67657 68124 99.3% 57.9% 60.5% 239277 2.36 68.1% 77.0% 2% 0.770 30639
2.58 242190 72705 74122 98.1% 98.3% 99.0% 236846 1.43 117.1% 128.6% 7% 0.803 30649
2.42 238428 77085 79650 96.8% 120.7% 129.1% 229754 0.99 145.1% 171.0% 2% 0.722 30257
2.28 173335 71749 84693 84.7% 135.3% 148.3% 156322 0.71 169.5% 218.7% 3% 0.706 21590
total 1728152 506121 524179 96.6% 18.6% 19.2% 1693662 5.43 22.0% 43.1% 3% 0.784 216305
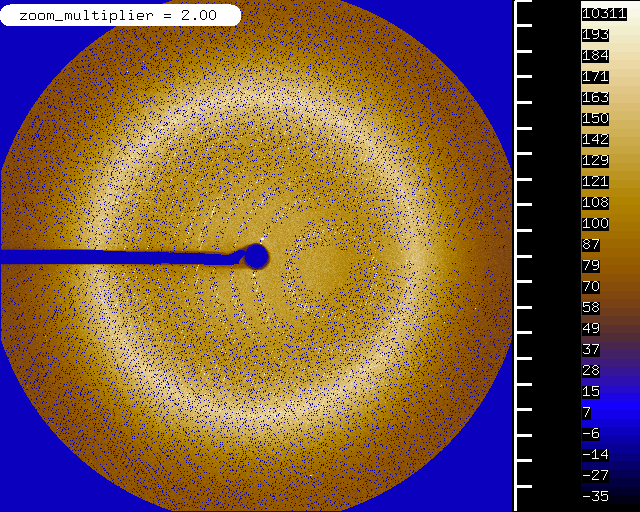
and there are few reflections missing in the blind region:
Finally, we may take a look at FRAME.pck and see that very few reflections are missing. The resolution of this image is not good enough to actually see the circles but one can see that all observed reflections are indeed hit by predictions.
From looking at rf.pck of many datasets, it is my experience that at the SLS (beamline X06SA), the R-factors along the spindle are better than perpendicular to it, which is quite surprising (and should be investigated). Therefore it is clear that in particular for these data it is a good thing to decrease MINIMUM_ZETA because accurately measured reflections are added to the data set.