CC1/2: Difference between revisions
No edit summary |
|||
| Line 9: | Line 9: | ||
== value of CC1/2 at a resolution where the signal vanishes == | == value of CC1/2 at a resolution where the signal vanishes == | ||
At a resolution where the signal vanishes, CC1/2 should be around zero. However, empirically we sometimes see negative values of CC1/2 (to values down to around -0.4) when using | At a resolution where the signal vanishes, CC1/2 should be around zero. However, empirically we sometimes see negative values of CC1/2 (to values down to around -0.4) when using SFTOOLS or PHENIX.CC_STAR for calculating it. On the other hand, CC1/2 as printed out in CORRECT.LP does approach zero. How can this be understood? | ||
The reason is that CORRECT does "alien" rejection (as documented in [[CORRECT.LP]]) ''after'' the final statistics table is printed. "Aliens" are reflections that are much stronger than should be expected in their resolution range, e.g. ice reflections. These reflections are identified in the following way: the average intensity in a resolution range is calculated. Any (acentric) reflection whose intensity is larger than 10 times the average is suspicious/unexpected; it is printed out at the bottom of CORRECT.LP (for centrics, the criterion is a bit different). By default, the parameter REJECT_ALIENS has a value of 20, which means that those reflections with intensity > 20*average are marked as aliens (outliers), and are disregarded in downstream processing (e.g. [[XDSCONV]]). | The reason is that CORRECT does "alien" rejection (as documented in [[CORRECT.LP]]) ''after'' the final statistics table is printed. "Aliens" are reflections that are much stronger than should be expected in their resolution range, e.g. ice reflections. These reflections are identified in the following way: the average intensity in a resolution range is calculated. Any (acentric) reflection whose intensity is larger than 10 times the average is suspicious/unexpected; it is printed out at the bottom of CORRECT.LP (for centrics, the criterion is a bit different). By default, the parameter REJECT_ALIENS has a value of 20, which means that those reflections with intensity > 20*average are marked as aliens (outliers), and are disregarded in downstream processing (e.g. [[XDSCONV]]). | ||
| Line 15: | Line 15: | ||
This is useful for identifying ice reflections if the average intensity/noise is high enough. However, in a resolution shell where the noise is much stronger than the signal (empirically, if the average I/sigma is less than 0.2), many reflections are considered as aliens - those where the noise happens to be strongly positive. If these are rejected (i.e. if the default REJECT_ALIEN is applied) then the average intensity even may become negative. | This is useful for identifying ice reflections if the average intensity/noise is high enough. However, in a resolution shell where the noise is much stronger than the signal (empirically, if the average I/sigma is less than 0.2), many reflections are considered as aliens - those where the noise happens to be strongly positive. If these are rejected (i.e. if the default REJECT_ALIEN is applied) then the average intensity even may become negative. | ||
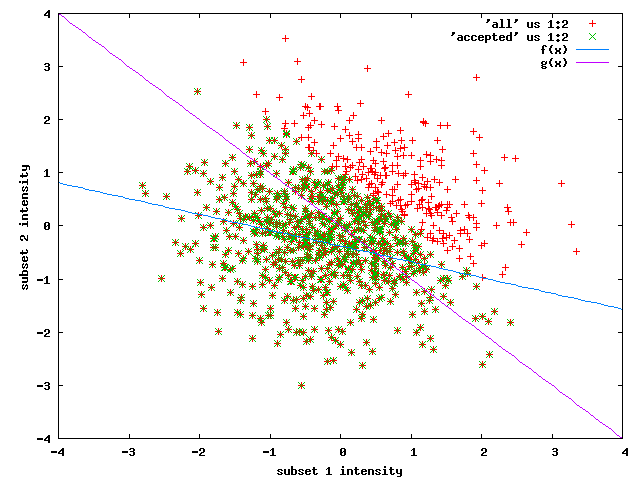
In addition, CC1/2 becomes negative as can be seen in a simulation that should clarify the principle. It employs random numbers that are normally distributed, with an average of 0.05 and a variance of one. In the figure below, each reflection is represented at a location determined by the intensities of its two subsets. Reflections with total intensity>1 are rejected (red crosses), whereas reflections with intensity<1 are used for calculating CC1/2 (green). The magenta line divides the plot into reflections with positive (total) intensity (upper right) and negative (total) intensity (lower left). The blue line is a least-squares fit to the "green" reflections; the correlation coefficient is -0.3. | In addition, CC1/2 becomes negative as can be seen in a simulation that should clarify the principle. It employs random numbers that are normally distributed, with an average of 0.05 and a variance of one. In the figure below, each reflection is represented at a location determined by the intensities of its two subsets. Reflections with total intensity>1 are rejected (red crosses), whereas reflections with intensity<1 are used for calculating CC1/2 (green). The magenta line divides the plot into reflections with positive (total) intensity (upper right) and negative (total) intensity (lower left). The blue line is a least-squares fit to the "green" reflections; the correlation coefficient is -0.3 (while that of all reflections is close to 0.0). | ||
To ensure that this type of rejection does not take place, one should specify REJECT_ALIENS=20000 | To ensure that this type of rejection does not take place, one should e.g. specify REJECT_ALIENS=20000 in XDS.INP. To obtain the statistics ''after'' rejecting aliens, one could use [[XSCALE]]. | ||
[[File:Reject_aliens.png]] | [[File:Reject_aliens.png]] | ||
Revision as of 22:14, 21 January 2013
number of reflection pairs
CORRECT.LP and XSCALE.LP do not explicitly state the number of reflection pairs that were used to calculated CC1/2..
However, the number can be calculated from the numbers available, for each resolution shell: there is the NUMBER OF UNIQUE REFLECTIONS (X), the NUMBER OF OBSERVED REFLECTIONS (Y), and the number of COMPARED reflections (Z) - the latter number is the total number of unmerged observations that contributed to the CC1/2 and the R-value calculations.
The number of reflections pairs that were used for the CC1/2 calculation can therefore be obtained as follows: Y-Z gives the number of unique reflections that have a single observation. The remaining (X-Y+Z) unique reflections have multiple observations, i.e. there were (X-Y+Z) reflection pairs that went into CC1/2.
value of CC1/2 at a resolution where the signal vanishes
At a resolution where the signal vanishes, CC1/2 should be around zero. However, empirically we sometimes see negative values of CC1/2 (to values down to around -0.4) when using SFTOOLS or PHENIX.CC_STAR for calculating it. On the other hand, CC1/2 as printed out in CORRECT.LP does approach zero. How can this be understood?
The reason is that CORRECT does "alien" rejection (as documented in CORRECT.LP) after the final statistics table is printed. "Aliens" are reflections that are much stronger than should be expected in their resolution range, e.g. ice reflections. These reflections are identified in the following way: the average intensity in a resolution range is calculated. Any (acentric) reflection whose intensity is larger than 10 times the average is suspicious/unexpected; it is printed out at the bottom of CORRECT.LP (for centrics, the criterion is a bit different). By default, the parameter REJECT_ALIENS has a value of 20, which means that those reflections with intensity > 20*average are marked as aliens (outliers), and are disregarded in downstream processing (e.g. XDSCONV).
This is useful for identifying ice reflections if the average intensity/noise is high enough. However, in a resolution shell where the noise is much stronger than the signal (empirically, if the average I/sigma is less than 0.2), many reflections are considered as aliens - those where the noise happens to be strongly positive. If these are rejected (i.e. if the default REJECT_ALIEN is applied) then the average intensity even may become negative.
In addition, CC1/2 becomes negative as can be seen in a simulation that should clarify the principle. It employs random numbers that are normally distributed, with an average of 0.05 and a variance of one. In the figure below, each reflection is represented at a location determined by the intensities of its two subsets. Reflections with total intensity>1 are rejected (red crosses), whereas reflections with intensity<1 are used for calculating CC1/2 (green). The magenta line divides the plot into reflections with positive (total) intensity (upper right) and negative (total) intensity (lower left). The blue line is a least-squares fit to the "green" reflections; the correlation coefficient is -0.3 (while that of all reflections is close to 0.0).
To ensure that this type of rejection does not take place, one should e.g. specify REJECT_ALIENS=20000 in XDS.INP. To obtain the statistics after rejecting aliens, one could use XSCALE.