1Y13
The structure is deposited in the PDB, solved with SAD and refined at a resolution of 2.2 A in spacegroup P4(3)2(1)2 (#96). The data for this project were provided by Jürgen Bosch (SGPP) and are linked to the ACA 2011 workshop website and here. There are two high-resolution (2 Å) datasets E1 (wavelength 0.9794Å) and E2 (@ 0.9174Å) collected (with 0.25° increments) at an ALS beamline on June 27, 2004, and a weaker dataset collected earlier at a SSRL beamline. We will only use the former two datasets here.
Dataset E1
Use generate_XDS.INP and run xds once. Based on R-factors in the resulting CORRECT.LP, and an inspection of BKGPIX.cbf, I modified XDS.INP to have
INCLUDE_RESOLUTION_RANGE=40 2.1 ! too weak beyond 2.1 Å VALUE_RANGE_FOR_TRUSTED_DETECTOR_PIXELS=8000. 30000. ! raised from 7000 30000 to mask beamstop
and ran xds again.
What's the problem?
This is the excerpt from CORRECT.LP :
SPACE-GROUP UNIT CELL CONSTANTS UNIQUE Rmeas COMPARED LATTICE-
NUMBER a b c alpha beta gamma CHARACTER
5 145.8 145.7 131.4 90.0 90.0 90.0 9735 24.5 23176 10 mC
75 103.1 103.1 131.4 90.0 90.0 90.0 5262 23.4 27649 11 tP
89 103.1 103.1 131.4 90.0 90.0 90.0 2911 22.8 30000 11 tP
21 145.7 145.8 131.4 90.0 90.0 90.0 5270 23.2 27641 13 oC
5 145.7 145.8 131.4 90.0 90.0 90.0 9681 24.2 23230 14 mC
1 102.9 103.2 131.4 90.0 90.0 89.9 18040 6.9 14871 31 aP
* 16 102.9 103.2 131.4 90.0 90.0 90.0 5568 9.1 27343 32 oP
3 103.2 102.9 131.4 90.0 90.0 90.0 10536 9.5 22375 35 mP
3 102.9 103.2 131.4 90.0 90.0 90.0 10496 8.3 22415 33 mP
3 102.9 131.4 103.2 90.0 90.1 90.0 9770 7.3 23141 34 mP
1 102.9 103.2 131.4 90.0 90.0 90.1 18040 6.9 14871 44 aP
...
REFINED PARAMETERS: DISTANCE BEAM ORIENTATION CELL AXIS
USING 219412 INDEXED SPOTS
STANDARD DEVIATION OF SPOT POSITION (PIXELS) 1.01
STANDARD DEVIATION OF SPINDLE POSITION (DEGREES) 0.11
CRYSTAL MOSAICITY (DEGREES) 0.191
DIRECT BEAM COORDINATES (REC. ANGSTROEM) -0.004789 0.003758 1.021015
DETECTOR COORDINATES (PIXELS) OF DIRECT BEAM 1027.25 1064.20
DETECTOR ORIGIN (PIXELS) AT 1036.84 1056.68
CRYSTAL TO DETECTOR DISTANCE (mm) 209.38
LAB COORDINATES OF DETECTOR X-AXIS 1.000000 0.000000 0.000000
LAB COORDINATES OF DETECTOR Y-AXIS 0.000000 1.000000 0.000000
LAB COORDINATES OF ROTATION AXIS 0.999997 0.000527 0.002187
COORDINATES OF UNIT CELL A-AXIS 21.922 52.895 85.337
COORDINATES OF UNIT CELL B-AXIS 3.771 87.158 -54.992
COORDINATES OF UNIT CELL C-AXIS -128.130 18.914 21.191
REC. CELL PARAMETERS 0.009731 0.009697 0.007620 90.000 90.000 90.000
UNIT CELL PARAMETERS 102.766 103.125 131.241 90.000 90.000 90.000
E.S.D. OF CELL PARAMETERS 1.3E-01 8.6E-02 9.3E-02 0.0E+00 0.0E+00 0.0E+00
SPACE GROUP NUMBER 16
So CORRECT chooses an orthorhombic spacegroup.
The file continues:
...
a b ISa
6.058E+00 3.027E-04 23.35
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
6.23 17389 5807 6045 96.1% 2.4% 2.8% 17277 35.83 3.0% 2.0% 66% 1.553 2434
4.43 32116 10536 10787 97.7% 2.7% 3.0% 32057 33.78 3.3% 2.4% 55% 1.272 4762
3.62 41900 13700 13961 98.1% 3.4% 3.4% 41793 27.98 4.1% 3.6% 38% 1.115 6295
3.14 51146 16371 16513 99.1% 5.4% 5.3% 50967 18.89 6.6% 7.2% 20% 0.961 7625
2.81 59159 18627 18675 99.7% 12.7% 13.2% 58877 9.82 15.4% 18.0% 8% 0.818 8716
2.56 65525 20596 20651 99.7% 28.5% 30.2% 65130 5.19 34.5% 40.4% 3% 0.757 9629
2.37 71579 22491 22533 99.8% 62.6% 67.1% 71068 2.60 75.6% 88.8% 1% 0.694 10498
2.22 74065 23837 24094 98.9% 97.9% 97.0% 73444 1.59 118.8% 139.8% 11% 0.738 11051
2.09 65776 24379 25674 95.0% 133.3% 140.6% 63647 0.90 166.4% 216.0% 1% 0.651 10380
total 478655 156344 158933 98.4% 6.5% 6.8% 474260 10.65 7.9% 22.5% 16% 0.852 71390
NUMBER OF REFLECTIONS IN SELECTED SUBSET OF IMAGES 492346
NUMBER OF REJECTED MISFITS 13342
NUMBER OF SYSTEMATIC ABSENT REFLECTIONS 0
NUMBER OF ACCEPTED OBSERVATIONS 479004
NUMBER OF UNIQUE ACCEPTED REFLECTIONS 157108
Some comments:
- the "STANDARD DEVIATION OF SPOT POSITION (PIXELS)" is significantly higher (1.01) than those reported for the 5°-batches in INTEGRATE.LP (about 0.6) . This suggests that the geometry refinement has to deal with inconsistent data.
- CORRECT obviously indicates an orthorhombic spacegroup.
- the number of MISFITS is higher than 1%. From the first long table (fine-grained in resolution) table in CORRECT.LP we learn that the misfits are due to faint high-resolution ice rings - so this is a problem intrinsic to the data, and not to their mode of processing.
To my surprise, pointless ("pointless xdsin XDS_ASCII.HKL") does not agree with CORRECT's standpoint:
Scores for each symmetry element
Nelmt Lklhd Z-cc CC N Rmeas Symmetry & operator (in Lattice Cell)
1 0.959 9.91 0.99 65030 0.034 identity
2 0.959 9.91 0.99 132222 0.035 *** 2-fold l ( 0 0 1) {-h,-k,+l}
3 0.958 9.87 0.99 110073 0.044 *** 2-fold h ( 1 0 0) {+h,-k,-l}
4 0.942 9.55 0.96 132646 0.109 *** 2-fold ( 1 1 0) {+k,+h,-l}
5 0.958 9.87 0.99 111819 0.043 *** 2-fold k ( 0 1 0) {-h,+k,-l}
6 0.941 9.54 0.95 131842 0.109 *** 2-fold ( 1-1 0) {-k,-h,-l}
7 0.937 9.50 0.95 224393 0.107 *** 4-fold l ( 0 0 1) {-k,+h,+l} {+k,-h,+l}
and
Laue Group Lklhd NetZc Zc+ Zc- CC CC- Rmeas R- Delta ReindexOperator > 1 P 4/m m m *** 1.000 9.73 9.73 0.00 0.97 0.00 0.07 0.00 0.2 [h,k,l] - 2 P m m m 0.000 0.35 9.88 9.53 0.99 0.95 0.04 0.11 0.0 [h,k,l] 3 C m m m 0.000 -0.02 9.72 9.74 0.97 0.97 0.07 0.07 0.2 [h+k,-h+k,l] 4 P 4/m 0.000 0.07 9.77 9.70 0.98 0.97 0.06 0.08 0.2 [h,k,l] 5 P 1 2/m 1 0.000 0.25 9.91 9.66 0.99 0.97 0.03 0.08 0.0 [-h,-l,-k] 6 P 1 2/m 1 0.000 0.22 9.89 9.67 0.99 0.97 0.04 0.08 0.0 [h,k,l] 7 P 1 2/m 1 0.000 0.21 9.88 9.67 0.99 0.97 0.04 0.08 0.0 [-k,-h,-l] 8 C 1 2/m 1 0.000 -0.01 9.72 9.73 0.97 0.97 0.07 0.07 0.2 [h-k,h+k,l] 9 C 1 2/m 1 0.000 -0.02 9.71 9.73 0.97 0.97 0.07 0.07 0.2 [h+k,-h+k,l] 10 P -1 0.000 0.21 9.91 9.70 0.99 0.97 0.03 0.08 0.0 [h,k,l]
and
Spacegroup TotProb SysAbsProb Reindex Conditions
<P 41 21 2> ( 92) 0.823 0.823 00l: l=4n, h00: h=2n (zones 1,2)
<P 43 21 2> ( 96) 0.823 0.823 00l: l=4n, h00: h=2n (zones 1,2)
..........
<P 4 21 2> ( 90) 0.095 0.095 h00: h=2n (zone 2)
..........
<P 42 21 2> ( 94) 0.077 0.077 00l: l=2n, h00: h=2n (zones 1,2)
Thus suggesting #92 or #96 - the latter of which agrees with the PDB deposition. However, running CORRECT in #96 and specifying 103 103 130 90 90 90 as cell parameters, we obtain:
REFINED PARAMETERS: DISTANCE BEAM ORIENTATION CELL AXIS
USING 220320 INDEXED SPOTS
STANDARD DEVIATION OF SPOT POSITION (PIXELS) 1.17
STANDARD DEVIATION OF SPINDLE POSITION (DEGREES) 0.14
CRYSTAL MOSAICITY (DEGREES) 0.191
DIRECT BEAM COORDINATES (REC. ANGSTROEM) -0.004790 0.004009 1.021014
DETECTOR COORDINATES (PIXELS) OF DIRECT BEAM 1027.19 1064.23
DETECTOR ORIGIN (PIXELS) AT 1036.79 1056.20
CRYSTAL TO DETECTOR DISTANCE (mm) 209.52
LAB COORDINATES OF DETECTOR X-AXIS 1.000000 0.000000 0.000000
LAB COORDINATES OF DETECTOR Y-AXIS 0.000000 1.000000 0.000000
LAB COORDINATES OF ROTATION AXIS 0.999996 0.000901 0.002534
COORDINATES OF UNIT CELL A-AXIS 21.926 53.087 85.553
COORDINATES OF UNIT CELL B-AXIS 3.794 87.060 -54.995
COORDINATES OF UNIT CELL C-AXIS -128.212 18.926 21.115
REC. CELL PARAMETERS 0.009704 0.009704 0.007616 90.000 90.000 90.000
UNIT CELL PARAMETERS 103.045 103.045 131.310 90.000 90.000 90.000
E.S.D. OF CELL PARAMETERS 2.1E-01 2.1E-01 2.1E-01 0.0E+00 0.0E+00 0.0E+00
SPACE GROUP NUMBER 96
...
a b ISa
7.890E+00 8.793E-04 12.01
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
6.23 16770 2983 3017 98.9% 5.2% 6.1% 16752 26.20 5.7% 2.6% 55% 1.247 1223
4.43 30598 5392 5393 100.0% 5.8% 6.2% 30596 25.25 6.3% 3.0% 50% 1.072 2420
3.62 39822 6992 6994 100.0% 6.9% 6.6% 39820 22.27 7.6% 4.0% 32% 0.975 3215
3.14 49620 8240 8242 100.0% 9.2% 8.7% 49619 17.14 10.1% 6.2% 19% 0.876 3847
2.81 59388 9379 9379 100.0% 17.7% 18.1% 59387 10.44 19.3% 12.3% 0% 0.736 4410
2.56 65652 10308 10310 100.0% 34.6% 39.1% 65652 6.08 37.7% 23.6% -1% 0.680 4872
2.37 71744 11258 11259 100.0% 71.3% 83.8% 71744 3.23 77.6% 52.1% -2% 0.652 5352
2.22 74888 12065 12082 99.9% 111.0% 116.9% 74888 1.98 121.2% 86.9% 2% 0.718 5753
2.09 65727 12386 12874 96.2% 151.3% 176.1% 65517 1.12 168.0% 148.4% -3% 0.631 5797
total 474209 79003 79550 99.3% 10.3% 11.0% 473975 9.44 11.3% 17.2% 13% 0.772 36889
NUMBER OF REFLECTIONS IN SELECTED SUBSET OF IMAGES 492346
NUMBER OF REJECTED MISFITS 17898
NUMBER OF SYSTEMATIC ABSENT REFLECTIONS 141
NUMBER OF ACCEPTED OBSERVATIONS 474307
NUMBER OF UNIQUE ACCEPTED REFLECTIONS 79022
which is much worse than the spacegroup 19 statistics (compare the ISa values - they differ by a factor of 2 !) so there may be something wrong with some assumptions we were making ...
Identifying a possible cause
The easiest thing one can do is to inspect INTEGRATE.LP - this lists scale factor, beam divergence and mosaicity for every reflection. There's a jiffy called "scalefactors" which grep's the relevant lines from INTEGRATE.LP ("scalefactors > scales.log"). This shows the scale factor (column 3):
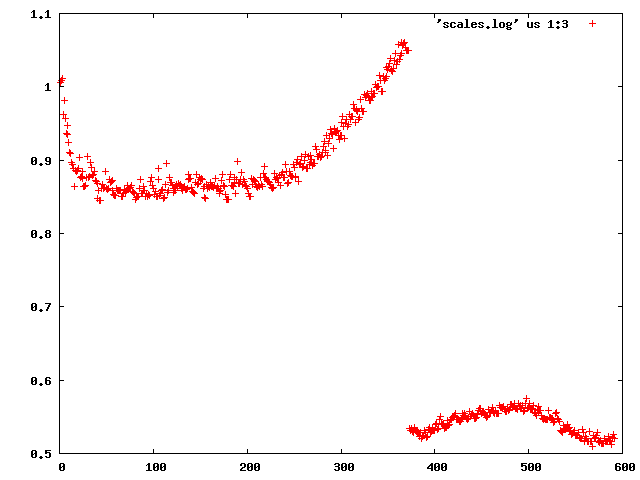
demonstrating that "something happens" between frame 372 and 373 (of course one has to look at the table to find the exact numbers).
It should be noted that any abrupt change in conditions during the experiment is going to spoil the resulting data in one way or another. This is most true for a SAD experiment which is supposed to give accurate values for the tiny differences in intensities between Friedel-related reflections.
A solution
At this point it is good to look at the data for experiment E2. Here, we find exactly the same problems of bad ISa and high "STANDARD DEVIATION OF SPOT POSITION (PIXELS)" when reducing frames 1-591 in one run of xds.
With this knowledge, we are lead, for E1, to reduce frames 1-372 and 373-592 separately, in spacegroup 96. For E2, we use frames 1-369 and 371-591, respectively. Frame E2-370 has a very high scale factor so we leave it out altogether.
This is also a good time to closely inspect the headers of the frames:
% grep --binary-files=text DATE j1603b3PK_1_E1_37?.img
gives
j1603b3PK_1_E1_370.img:DATE=Sun Jun 27 08:55:51 2004; j1603b3PK_1_E1_371.img:DATE=Sun Jun 27 08:56:00 2004; j1603b3PK_1_E1_372.img:DATE=Sun Jun 27 08:56:08 2004; j1603b3PK_1_E1_373.img:DATE=Sun Jun 27 09:19:45 2004; j1603b3PK_1_E1_374.img:DATE=Sun Jun 27 09:19:54 2004; j1603b3PK_1_E1_375.img:DATE=Sun Jun 27 09:20:02 2004; j1603b3PK_1_E1_376.img:DATE=Sun Jun 27 09:20:10 2004; j1603b3PK_1_E1_377.img:DATE=Sun Jun 27 09:20:58 2004; j1603b3PK_1_E1_378.img:DATE=Sun Jun 27 09:21:08 2004; j1603b3PK_1_E1_379.img:DATE=Sun Jun 27 09:21:17 2004;
and
% grep --binary-files=text DATE j1603b3PK_1_E2_3[67]?.img
gives
j1603b3PK_1_E2_366.img:DATE=Sun Jun 27 08:55:15 2004; j1603b3PK_1_E2_367.img:DATE=Sun Jun 27 08:55:23 2004; j1603b3PK_1_E2_368.img:DATE=Sun Jun 27 08:55:32 2004; j1603b3PK_1_E2_369.img:DATE=Sun Jun 27 08:56:19 2004; j1603b3PK_1_E2_370.img:DATE=Sun Jun 27 08:56:28 2004; j1603b3PK_1_E2_371.img:DATE=Sun Jun 27 09:19:26 2004; j1603b3PK_1_E2_372.img:DATE=Sun Jun 27 09:19:34 2004; j1603b3PK_1_E2_373.img:DATE=Sun Jun 27 09:20:22 2004; j1603b3PK_1_E2_374.img:DATE=Sun Jun 27 09:20:30 2004; j1603b3PK_1_E2_375.img:DATE=Sun Jun 27 09:20:38 2004; j1603b3PK_1_E2_376.img:DATE=Sun Jun 27 09:20:47 2004;
thus proving that both datasets were interrupted for 20 minutes around frame 370.
Interestingly, both datasets appear to be collected at the same time, but at different wavelengths (E1 at 0.9794 Å, E2 at 0.9184 Å), and yet the individual parts merge as follows: using the following XSCALE.INP:
UNIT_CELL_CONSTANTS=103.316 103.316 131.456 90.000 90.000 90.000 SPACE_GROUP_NUMBER=96 OUTPUT_FILE=temp.ahkl INPUT_FILE=../e1_1-372/XDS_ASCII.HKL INPUT_FILE=../e1_373-592/XDS_ASCII.HKL INPUT_FILE=../e2_1-369/XDS_ASCII.HKL INPUT_FILE=../e2_371-591/XDS_ASCII.HKL
and running xscale, we obtain in XSCALE.LP:
CORRELATIONS BETWEEN INPUT DATA SETS AFTER CORRECTIONS DATA SETS NUMBER OF COMMON CORRELATION RATIO OF COMMON B-FACTOR #i #j REFLECTIONS BETWEEN i,j INTENSITIES (i/j) BETWEEN i,j 1 2 15943 0.978 1.0002 0.0106 1 3 22366 1.000 1.0012 -0.0008 2 3 15801 0.977 0.9983 0.0557 1 4 15648 0.979 0.9988 0.0541 2 4 14862 0.999 1.0024 -0.0007 3 4 15524 0.978 0.9999 -0.0015
which means that e1_1-372 correlates well (1.000) with e2_1-369, and e1_373-59 well (0.999) with e2_371-591, but the crosswise correlations are consistently low (0.978, 0.977, 0.979, 0.978). The adjustment to the error model proves this:
a b ISa ISa0 INPUT DATA SET 6.112E+00 1.429E-03 10.70 22.37 ../e1_1-372/XDS_ASCII.HKL 1.074E+01 1.825E-03 7.14 23.79 ../e1_373-592/XDS_ASCII.HKL 5.707E+00 1.621E-03 10.40 22.82 ../e2_1-369/XDS_ASCII.HKL 8.547E+00 1.796E-03 8.07 24.17 ../e2_371-591/XDS_ASCII.HKL
telling us that "if we merge these datasets together, their error estimates have to be increased a lot". However, if we switch to
UNIT_CELL_CONSTANTS=103.316 103.316 131.456 90.000 90.000 90.000 SPACE_GROUP_NUMBER=96 OUTPUT_FILE=firstparts.ahkl INPUT_FILE=../e1_1-372/XDS_ASCII.HKL INPUT_FILE=../e2_1-369/XDS_ASCII.HKL OUTPUT_FILE=secondparts.ahkl INPUT_FILE=../e1_373-592/XDS_ASCII.HKL INPUT_FILE=../e2_371-591/XDS_ASCII.HKL
we obtain
a b ISa ISa0 INPUT DATA SET 6.120E+00 3.673E-04 21.09 22.37 ../e1_1-372/XDS_ASCII.HKL 5.713E+00 3.819E-04 21.41 22.82 ../e2_1-369/XDS_ASCII.HKL 5.639E+00 3.151E-04 23.72 23.79 ../e1_373-592/XDS_ASCII.HKL 5.289E+00 3.258E-04 24.09 24.17 ../e2_371-591/XDS_ASCII.HKL
proving that the second parts of datasets E1 and E2 should be treated separately from the first parts.
Upon inspection of the cell parameters, we find that the cell axes of the second "halfs" are shorter by a factor of 0.9908 when compared with the first parts. This suggests that they were collected at a longer wavelength, or that radiation damage changed the cell parameters during the 20-minute break - usually it makes them longer (Ravelli et al. (2002), J. Synchrotron Rad. 9, 355-360), but this may be the exception to the rule! Maybe the crystal even was exposed to the beam during that time, in an attempt to try radiation-damage induced phasing (see e.g. Ravelli et al Structure 11 (2003), 217-220).
The almost-simultaneous DATEs in the headers may be explained by a wavelength-switching measuring strategy which alternatingly collects 4 frames at one wavelength as E1, then changes the wavelength and collects 4 frames into E2.
So this little detective work appears to give us useful information about what happened in the morning of Sunday June 27, 2004 at ALS beamline 821 - but some questions remain.
Further analysis of datasets E1 and E2
Here, we try to learn more about the constituents of "firstparts".
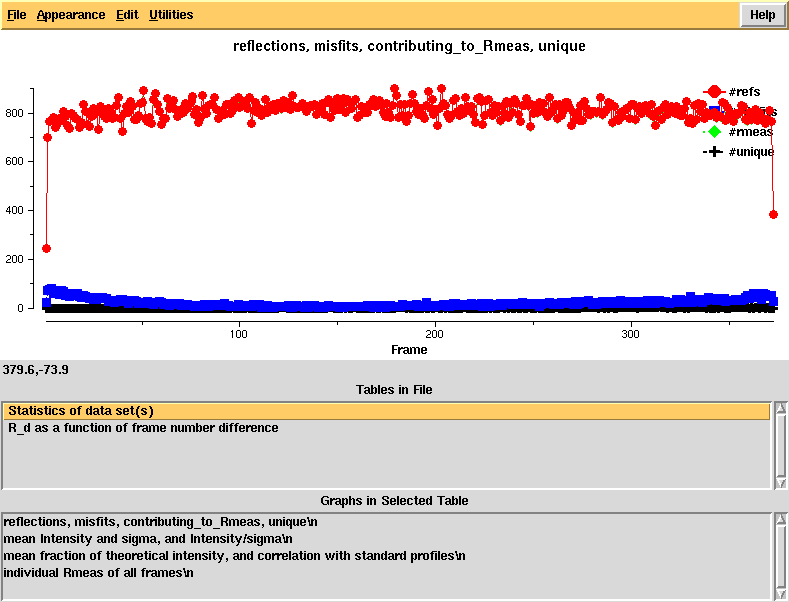
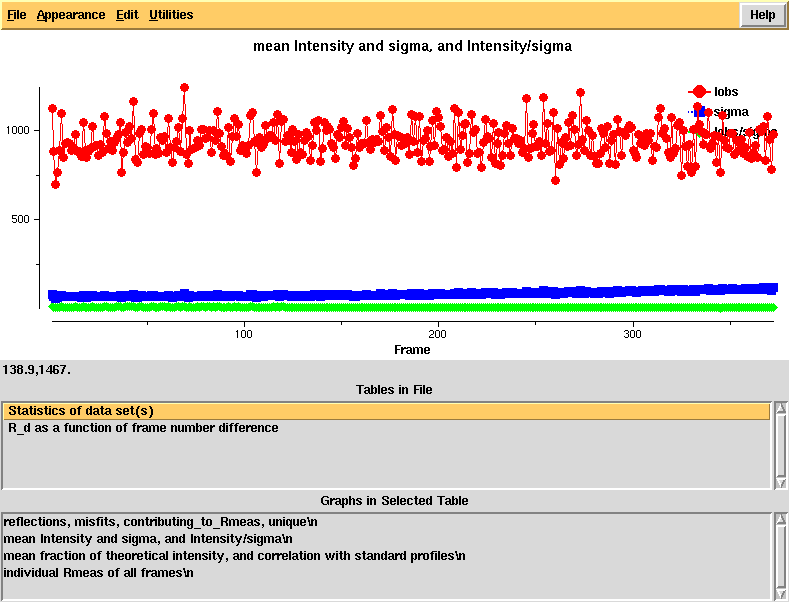
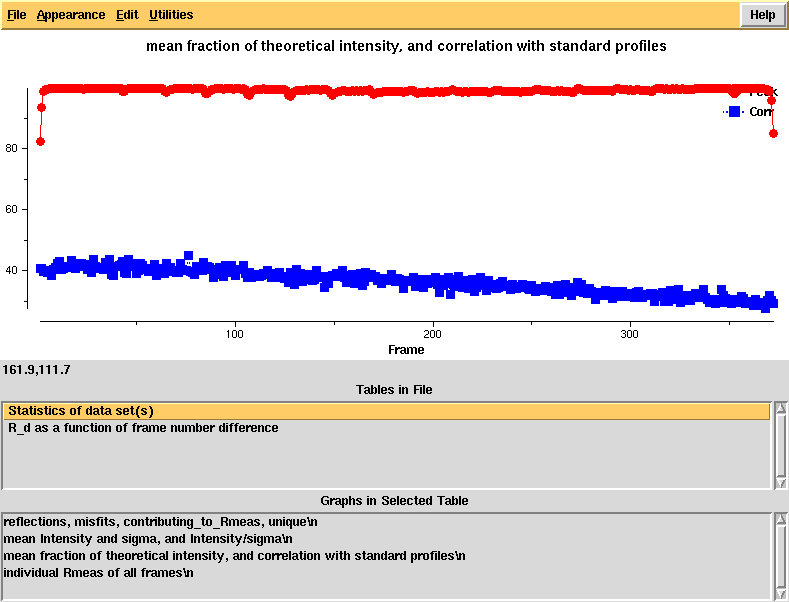
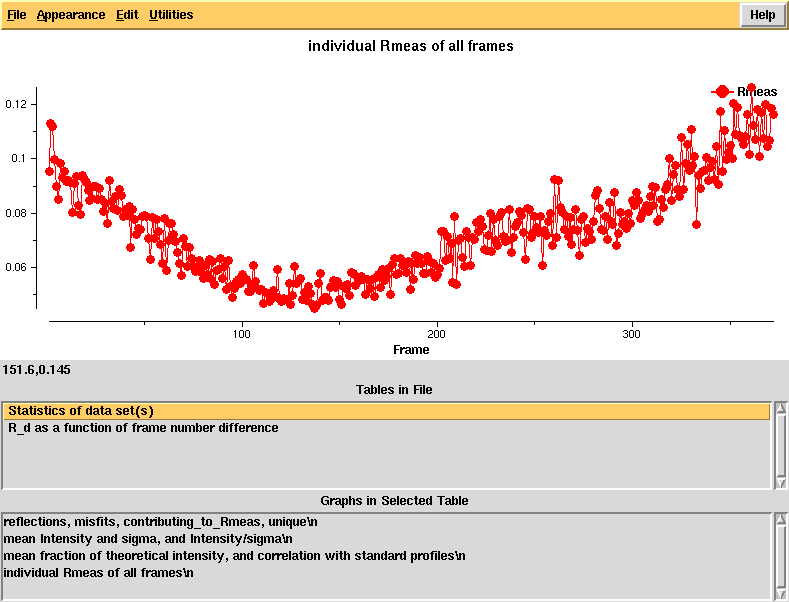
Running "xdsstat > XDSSTAT.LP" in the e1_1-372 and e2_1-369 directories, we obtain statistics output not available from CORRECT. We open XDSSTAT.LP with the CCP4 program "loggraph", and take a look at misfits.pck, rf.pck, and the other files produced by xdsstat, using VIEW or XDS-Viewer:
Reflections and misfits, by frame - looks normal
Intensity and sigma by frame - looks normal
"partiality" and profile agreement, by frame - looks good but it's clear that the profiles at high frame number agree worse with the average profiles, possibly due to radiation damage
R_meas, by frame, clearly showing good R_meas in the middle of the dataset
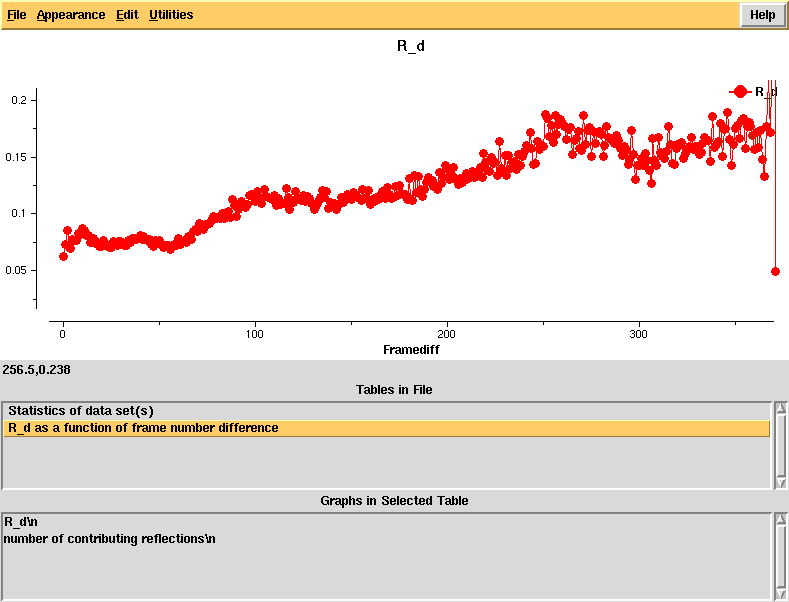
R_d - an R-factor which directly depends on radiation damage. This is calculated as a function of frame number difference and the linear rise indicates significant radiation damage that should be correctable in XSCALE, using the CRYSTAL_NAME keyword.
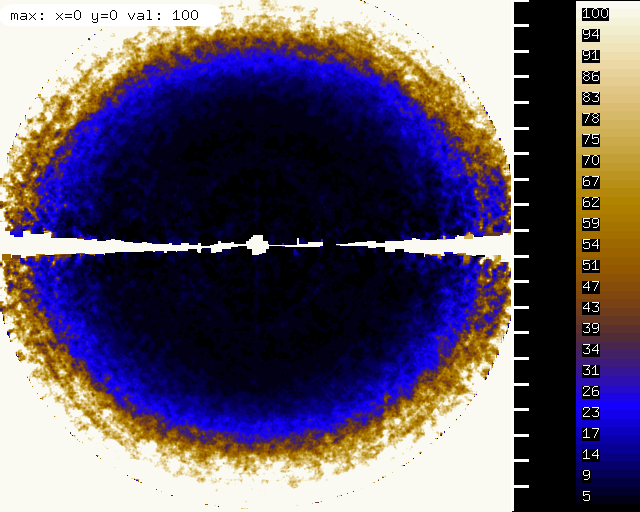
misfits mapped on the detector, showing ice rings.
R_meas mapped on the detector, showing elevated R_meas at the location of the ice rings.
Solving the structure
It appears reasonable to discard the "second parts" since they are strongly influenced by radiation damage. Then, we could
- merge together (into one output file) the two first parts of E1 and E2, thus obtaining a single pseudo-SAD dataset. The reason for doing this is that the anomalous signal of both datasets is so strong, and their (isomorphous) difference is weak (after all, the correlation coefficient is 1.000 !)
- keep the first parts of E1 (inflection, according to the documentation) and E2 (high-enery remote) separate, and treat them as MAD (or rather, DAD).
First try at pseudo-SAD
Let's look at the XSCALE statistics for the merged-together "firstparts":
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
9.40 6122 844 883 95.6% 2.9% 3.5% 6111 54.76 3.2% 1.4% 79% 2.137 313
6.64 12037 1611 1621 99.4% 2.9% 3.6% 12035 51.54 3.1% 1.5% 80% 2.259 684
5.43 15348 2065 2086 99.0% 3.5% 3.7% 15347 47.79 3.7% 1.7% 78% 2.294 908
4.70 18714 2487 2498 99.6% 3.0% 3.7% 18711 49.55 3.2% 1.5% 72% 1.712 1120
4.20 21104 2797 2821 99.1% 3.1% 3.7% 21102 47.24 3.3% 1.7% 72% 1.727 1271
3.84 23316 3095 3117 99.3% 3.8% 4.0% 23313 42.74 4.1% 2.1% 65% 1.617 1420
3.55 25693 3345 3366 99.4% 4.4% 4.5% 25693 37.93 4.7% 2.6% 50% 1.411 1548
3.32 28017 3633 3653 99.5% 5.2% 5.2% 28015 32.89 5.6% 3.6% 40% 1.335 1687
3.13 30266 3842 3848 99.8% 7.2% 7.2% 30264 25.87 7.7% 4.8% 36% 1.158 1797
2.97 32595 4114 4118 99.9% 10.4% 10.4% 32594 19.26 11.1% 7.7% 30% 1.068 1925
2.83 34384 4315 4320 99.9% 14.3% 14.8% 34382 14.88 15.3% 10.3% 20% 0.937 2031
2.71 35654 4475 4478 99.9% 18.3% 19.1% 35652 12.13 19.5% 13.1% 15% 0.891 2110
2.61 37307 4705 4710 99.9% 27.5% 28.8% 37304 8.44 29.4% 19.8% 11% 0.834 2224
2.51 38997 4893 4896 99.9% 35.5% 38.0% 38997 6.78 38.0% 26.0% 10% 0.817 2318
2.43 40036 5026 5027 100.0% 51.3% 55.1% 40032 4.92 54.8% 38.0% 2% 0.738 2387
2.35 39975 5180 5222 99.2% 71.3% 68.9% 39967 3.78 76.4% 52.7% 21% 0.887 2446
2.28 42041 5385 5423 99.3% 93.7% 93.1% 42037 2.90 100.3% 66.7% 11% 0.798 2548
2.21 43012 5538 5541 99.9% 85.7% 88.3% 43011 2.87 91.8% 58.8% 10% 0.818 2644
2.16 42610 5701 5703 100.0% 113.6% 120.7% 42607 2.13 122.0% 85.4% 4% 0.722 2724
2.10 38996 5634 5912 95.3% 146.1% 153.9% 38944 1.50 157.8% 122.7% 3% 0.711 2639
total 606224 78685 79243 99.3% 6.7% 7.2% 606118 16.88 7.2% 12.0% 29% 1.055 36744
The anomalous correlation is good at low resolution, though not outstanding. At high resolution it rises again but this is presumably due to the ice rings.
I like to use hkl2map which runs SHELXC, SHELXD and SHELXE from its GUI. Before doing so, we have to run XDSCONV with the following XDSCONV.INP:
INPUT_FILE=firstparts.hkl OUTPUT_FILE=temp.hkl SHELX
First, the shelxc output which shows that these data are quite good:
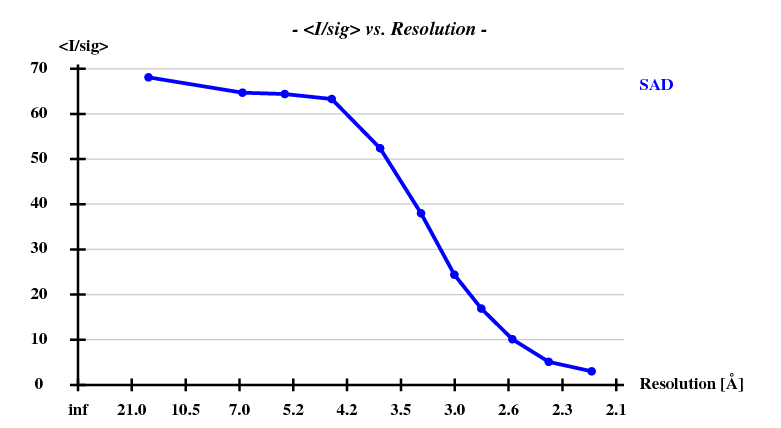
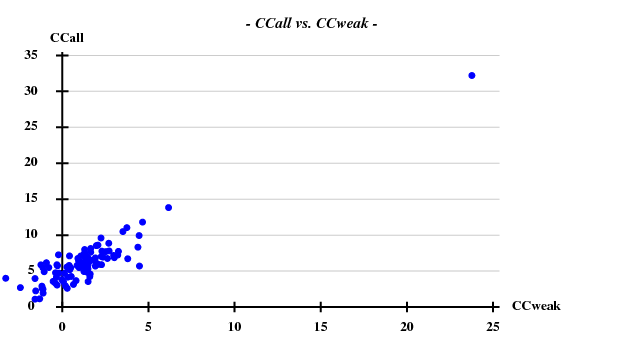
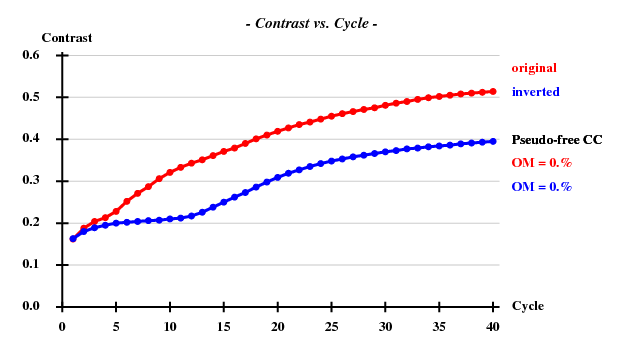
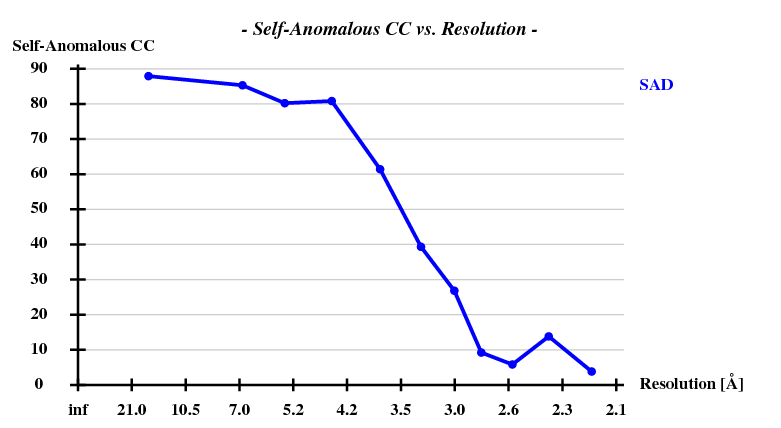And then we show the result of 100 trials at substructure solution of shelxd, trying to find 3 Se atoms at 30 - 3.3Å resolution (I also tried 3.0 3.1 3.2 3.4 3.5 Å but 3.3 Å was best).
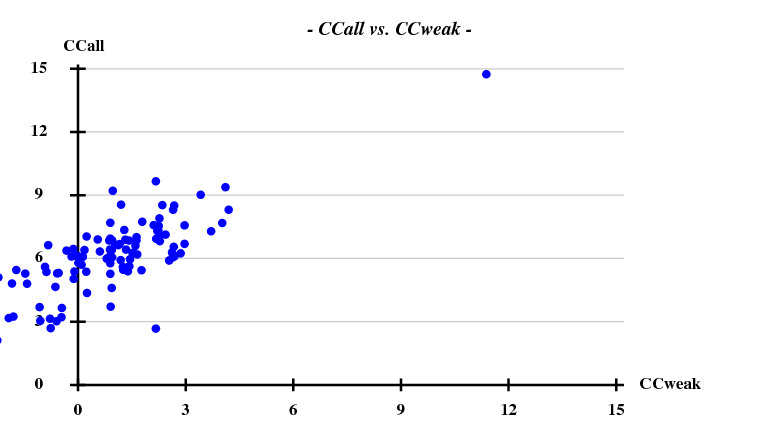
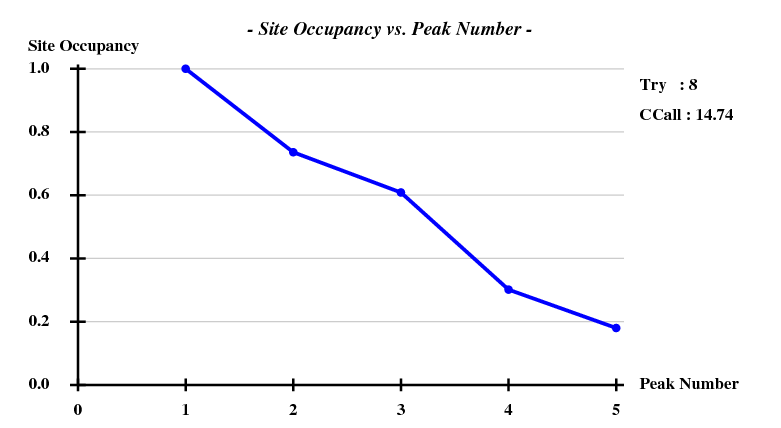
This looks reasonable although the absolute value of CCall is so low that there is little hope that the structure can be solved with this amount of information. And indeed, SHELXE did not show a difference between the two hands (in fact we even know that the "original hand" is the correct one since the inverted had would correspond to spacegroup #92 !).
Second try: correcting radiation damage by 0-dose extrapolation
Since we noted significant radiation damage we could try to correct that. All we have to do is ask XSCALE to do zero-dose extrapolation:
UNIT_CELL_CONSTANTS=103.316 103.316 131.456 90.000 90.000 90.000 SPACE_GROUP_NUMBER=96 OUTPUT_FILE=temp.ahkl INPUT_FILE=../e1_1-372/XDS_ASCII.HKL CRYSTAL_NAME=a INPUT_FILE=../e2_1-369/XDS_ASCII.HKL CRYSTAL_NAME=a
As a result we obtain in XSCALE.LP:
******************************************************************************
RESULTS FROM ZERO-DOSE EXTRAPOLATION OF REFLECTION INTENSITIES
for reference on this subject see:
K. Diederichs, S. McSweeney & R.B.G. Ravelli, Acta Cryst. D59, 903-909(2003).
"Zero-dose extrapolation as part of macromolecular synchrotron data reduction"
******************************************************************************
Radiation damage can lead to localized modifications of the structure.
To correct for this effect, XSCALE modifies the intensity measurements
I(h,i) by individual correction factors,
exp{-b(h)*dose(h,i)}
where h,i denotes the i-th observation with unique reflection indices
h, and dose(h,i) the X-ray dose accumulated by the crystal when the
reflection was recorded. Assuming a constant dose for each image
(dose_rate), the accumulated dose when recording image_number(i), on
which I(h,i) was observed, is then
dose(h,i) = starting_dose + dose_rate * (image_number(i)-first_image)
The decay factor b(h) is determined from the assumption that symmetry
related reflections in a data set taken from the same crystal should
have the same intensity after correction. Moreover, b(h) is assumed to
be the same for Friedel-pairs and independent of the X-ray wavelength.
To avoid overfitting the data, XSCALE starts with the hypothesis that
b(h)=0 and rejects this assumption if its probability is below 10.0%.
CORRELATION OF COMMON DECAY-FACTORS BETWEEN INPUT DATA SETS
-----------------------------------------------------------
First INPUT_FILE= ../e2_1-369/XDS_ASCII.HKL
CRYSTAL_NAME= a
Second INPUT_FILE= ../e1_1-372/XDS_ASCII.HKL
CRYSTAL_NAME= a
RESOLUTION NUMBER CORRELATION
LIMIT OF PAIRS FACTOR
9.40 210 0.955
6.64 441 0.955
5.43 587 0.940
4.70 692 0.969
4.20 750 0.949
3.84 836 0.920
3.55 809 0.942
3.32 775 0.925
3.13 663 0.888
2.97 557 0.837
2.83 375 0.681
2.71 302 0.812
2.61 212 0.625
2.51 163 0.508
2.43 95 0.291
2.35 139 0.722
2.28 110 0.688
2.21 91 0.734
2.16 88 0.561
2.10 54 0.126
total 7949 0.788
X-RAY DOSE PARAMETERS USED FOR EACH INPUT DATA SET
--------------------------------------------------
CRYSTAL_NAME= a
STARTING_DOSE DOSE_RATE NAME OF INPUT FILE
initial refined initial refined
0.000E+00 8.557E+00 1.000E+00 1.000E+00 ../e1_1-372/XDS_ASCII.HKL
0.000E+00 0.000E+00 1.000E+00 1.024E+00 ../e2_1-369/XDS_ASCII.HKL
STATISTICS OF 0-DOSE CORRECTED DATA FROM EACH CRYSTAL
-----------------------------------------------------
NUNIQUE = Number of unique reflections with enough symmetry-
related observations to determine a decay factor b(h)
N0-DOSE = Number of 0-dose extrapolated unique reflections
NERROR = Number of unique extrapolated reflections expected
to be overfitted. A large ratio of N0-DOSE/NERROR
justifies the data correction as carried out here.
S_corr = mean value of Sigma(I) for 0-dose extrapolated data
S_norm = mean value of Sigma(I) for the same data but
without 0-dose extrapolation.
NFREE = degrees of freedom for calculating S_corr
CRYSTAL_NAME= a
RESOLUTION NUNIQUE N0-DOSE N0-DOSE/ S_corr/ NFREE
LIMIT NERROR S_norm
9.40 496 378 68.0 0.543 3180
6.64 908 703 78.9 0.554 6245
5.43 1140 894 77.0 0.574 8064
4.70 1351 1040 77.4 0.599 9671
4.20 1518 1133 69.9 0.620 10585
3.84 1665 1187 73.9 0.630 11129
3.55 1787 1220 65.1 0.671 11917
3.32 1941 1289 58.1 0.690 12728
3.13 2042 1172 49.8 0.717 11877
2.97 2182 1103 48.1 0.750 11498
2.83 2281 911 40.1 0.798 9662
2.71 2352 812 34.2 0.825 8611
2.61 2467 702 34.1 0.848 7383
2.51 2566 627 31.5 0.875 6595
2.43 2624 499 31.2 0.895 5295
2.35 2709 629 31.6 0.888 6240
2.28 2821 603 28.5 0.893 6147
2.21 2880 560 32.4 0.905 5758
2.16 2959 448 30.3 0.907 4394
2.10 2860 413 29.9 0.924 3745
total 41549 16323 46.8 0.739 160724
******************************************************************************
SCALING FACTORS FOR Sigma(I) AS FUNCTION OF RESOLUTION
******************************************************************************
SCALING FACTORS FOR Sigma(I) FOR DATA SET ../e1_1-372/XDS_ASCII.HKL
RESOLUTION (ANGSTROM)
10.33 6.12 4.76 4.03 3.56 3.23 2.97 2.76 2.60 2.46 2.34 2.23 2.14
FACTOR 0.94 0.96 0.88 0.93 0.99 0.98 0.99 0.99 0.99 0.98 1.10 1.00 0.99
SCALING FACTORS FOR Sigma(I) FOR DATA SET ../e2_1-369/XDS_ASCII.HKL
RESOLUTION (ANGSTROM)
10.32 6.11 4.76 4.03 3.56 3.22 2.97 2.76 2.60 2.46 2.34 2.23 2.14
FACTOR 0.96 0.98 0.89 0.94 1.01 1.01 1.02 1.01 1.00 0.99 1.11 1.02 0.98
******************************************************************************
STATISTICS OF SCALED OUTPUT DATA SET : temp.ahkl
FILE TYPE: XDS_ASCII MERGE=FALSE FRIEDEL'S_LAW=FALSE
1270 OUT OF 607179 REFLECTIONS REJECTED
605909 REFLECTIONS ON OUTPUT FILE
******************************************************************************
DEFINITIONS:
R-FACTOR
observed = (SUM(ABS(I(h,i)-I(h))))/(SUM(I(h,i)))
expected = expected R-FACTOR derived from Sigma(I)
COMPARED = number of reflections used for calculating R-FACTOR
I/SIGMA = mean of intensity/Sigma(I) of unique reflections
(after merging symmetry-related observations)
Sigma(I) = standard deviation of reflection intensity I
estimated from sample statistics
R-meas = redundancy independent R-factor (intensities)
Rmrgd-F = quality of amplitudes (F) in the scaled data set
For definition of R-meas and Rmrgd-F see
Diederichs & Karplus (1997), Nature Struct. Biol. 4, 269-275.
Anomal = mean correlation factor between two random subsets
Corr of anomalous intensity differences
SigAno = mean anomalous difference in units of its estimated
standard deviation (|F(+)-F(-)|/Sigma). F(+), F(-)
are structure factor estimates obtained from the
merged intensity observations in each parity class.
Nano = Number of unique reflections used to calculate
Anomal_Corr & SigAno. At least two observations
for each (+ and -) parity are required.
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
9.40 6095 844 883 95.6% 2.0% 2.6% 6084 73.41 2.1% 0.9% 87% 2.706 313
6.64 12006 1611 1621 99.4% 2.0% 2.8% 12004 68.81 2.1% 1.0% 84% 2.555 684
5.43 15339 2065 2086 99.0% 2.2% 2.8% 15338 63.28 2.4% 1.2% 82% 2.409 908
4.70 18697 2486 2498 99.5% 1.9% 2.6% 18694 70.84 2.1% 1.0% 75% 1.855 1120
4.20 21080 2796 2821 99.1% 2.0% 2.7% 21078 66.87 2.1% 1.1% 67% 1.727 1270
3.84 23300 3094 3117 99.3% 2.5% 3.0% 23297 58.10 2.7% 1.5% 64% 1.551 1420
3.55 25676 3344 3366 99.3% 3.1% 3.6% 25676 48.56 3.4% 1.9% 50% 1.326 1548
3.32 28013 3633 3653 99.5% 3.9% 4.3% 28011 41.76 4.1% 2.8% 37% 1.244 1687
3.13 30254 3841 3848 99.8% 5.7% 6.0% 30252 32.18 6.1% 4.1% 35% 1.125 1796
2.97 32595 4114 4118 99.9% 8.8% 9.1% 32594 23.53 9.4% 6.8% 26% 1.038 1925
2.83 34368 4313 4320 99.8% 12.8% 13.3% 34366 17.65 13.6% 9.5% 21% 0.989 2030
2.71 35627 4472 4478 99.9% 16.9% 17.4% 35625 14.15 18.1% 12.2% 18% 0.965 2108
2.61 37300 4704 4710 99.9% 25.8% 26.4% 37297 9.70 27.6% 19.3% 16% 0.930 2223
2.51 38975 4890 4896 99.9% 33.8% 34.9% 38975 7.68 36.1% 24.1% 14% 0.888 2315
2.43 39971 5019 5027 99.8% 49.1% 50.8% 39967 5.47 52.5% 37.2% 8% 0.810 2380
2.35 39968 5179 5222 99.2% 67.9% 67.5% 39960 4.07 72.7% 50.4% 25% 0.927 2445
2.28 42067 5388 5423 99.4% 89.9% 94.3% 42063 3.03 96.2% 63.5% 16% 0.796 2548
2.21 43011 5538 5541 99.9% 82.3% 83.3% 43010 3.16 88.1% 57.9% 14% 0.871 2644
2.16 42577 5697 5703 99.9% 108.5% 112.2% 42574 2.37 116.6% 83.1% 3% 0.760 2720
2.10 38988 5633 5912 95.3% 142.1% 144.2% 38936 1.67 153.5% 119.2% 6% 0.772 2638
total 605907 78661 79243 99.3% 5.5% 6.1% 605801 21.72 5.9% 11.3% 27% 1.095 36722
We note that the "CORRELATION OF COMMON DECAY-FACTORS BETWEEN INPUT DATA SETS" are really high which confirms the hypothesis that this is a valid procedure to perform.
Comparison of the last table with that of the previous paragraph, i.e. without zero-dose extrapolation, shows that the I/sigma, the anomalous correlation coefficients and the SigAno are significantly higher. Does this translate into better structure solution? It does:
Automatically building the main chain of 452 out of 519 residues
Based on the sites obtained by SHELXD, we run
shelxe.beta -a -q -h -b -s0.585 -m40 raddam raddam_fa
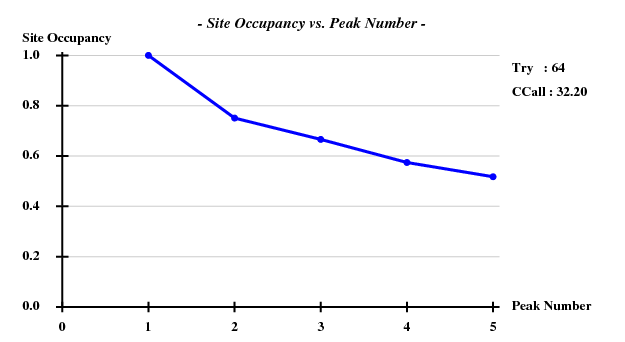
This already builds a significant number of residues, but also gives an improved list of heavy atom sites - there are actually 6 sites instead of the 5 that SHELXD wrote out (yes, we had asked SHELXD for 3 sites since there are 3 Met residues, but SHELXD as always was smarter than we are). We "mv raddam.hat raddam_fa.res" for another run of SHELXE:
shelxe.beta -a -q -h6 -b -s0.585 -m40 -n3 raddam raddam_fa
and get
452 residues left after pruning, divided into chains as follows:
A: 15 B: 5 C: 22 D: 22 E: 27 F: 62 G: 263 H: 36
CC for partial structure against native data = 39.83 %
------------------------------------------------------------------------------
Global autotracing cycle 4
<wt> = 0.300, Contrast = 0.447, Connect. = 0.705 for dens.mod. cycle 1
<wt> = 0.300, Contrast = 0.660, Connect. = 0.781 for dens.mod. cycle 2
<wt> = 0.300, Contrast = 0.723, Connect. = 0.801 for dens.mod. cycle 3
<wt> = 0.300, Contrast = 0.762, Connect. = 0.807 for dens.mod. cycle 4
Pseudo-free CC = 64.88 %
<wt> = 0.300, Contrast = 0.785, Connect. = 0.810 for dens.mod. cycle 5
<wt> = 0.300, Contrast = 0.806, Connect. = 0.813 for dens.mod. cycle 6
<wt> = 0.300, Contrast = 0.820, Connect. = 0.815 for dens.mod. cycle 7
<wt> = 0.300, Contrast = 0.831, Connect. = 0.817 for dens.mod. cycle 8
<wt> = 0.300, Contrast = 0.839, Connect. = 0.819 for dens.mod. cycle 9
Pseudo-free CC = 69.74 %
<wt> = 0.300, Contrast = 0.845, Connect. = 0.820 for dens.mod. cycle 10
<wt> = 0.300, Contrast = 0.849, Connect. = 0.821 for dens.mod. cycle 11
<wt> = 0.300, Contrast = 0.851, Connect. = 0.822 for dens.mod. cycle 12
<wt> = 0.300, Contrast = 0.853, Connect. = 0.823 for dens.mod. cycle 13
<wt> = 0.300, Contrast = 0.854, Connect. = 0.823 for dens.mod. cycle 14
Pseudo-free CC = 70.80 %
<wt> = 0.300, Contrast = 0.854, Connect. = 0.824 for dens.mod. cycle 15
<wt> = 0.300, Contrast = 0.855, Connect. = 0.824 for dens.mod. cycle 16
<wt> = 0.300, Contrast = 0.855, Connect. = 0.824 for dens.mod. cycle 17
<wt> = 0.300, Contrast = 0.854, Connect. = 0.824 for dens.mod. cycle 18
<wt> = 0.300, Contrast = 0.854, Connect. = 0.824 for dens.mod. cycle 19
Pseudo-free CC = 71.03 %
<wt> = 0.300, Contrast = 0.854, Connect. = 0.824 for dens.mod. cycle 20
Estimated mean FOM and mapCC as a function of resolution
d inf - 4.62 - 3.64 - 3.17 - 2.88 - 2.67 - 2.51 - 2.38 - 2.27 - 2.18 - 2.11
<FOM> 0.736 0.786 0.768 0.721 0.701 0.681 0.618 0.595 0.587 0.540
<mapCC> 0.862 0.932 0.946 0.934 0.924 0.924 0.922 0.913 0.882 0.858
N 4206 4227 4214 4135 4185 4207 4292 4406 4320 3702
Estimated mean FOM = 0.674 Pseudo-free CC = 71.18 %
Density (in map sigma units) at input heavy atom sites
Site x y z occ*Z density
1 0.2276 0.7578 0.1189 34.0000 29.98
2 0.1568 0.6345 0.3049 32.2898 30.44
3 0.1767 0.5344 0.2160 32.2388 29.67
4 0.3059 0.4535 0.1297 26.0746 23.51
5 0.0280 0.8243 0.1410 22.7324 21.02
6 0.0383 0.9748 0.0492 21.5050 21.18
Site x y z h(sig) near old near new
1 0.1569 0.6345 0.3048 30.4 2/0.02 9/13.36 3/15.73 2/19.52 7/22.13
2 0.2278 0.7578 0.1188 30.0 1/0.02 1/19.52 6/21.97 7/22.48 9/25.02
3 0.1767 0.5345 0.2158 29.7 3/0.03 9/2.90 1/15.73 4/19.45 2/26.88
4 0.3060 0.4536 0.1292 23.5 4/0.07 3/19.45 9/21.16 8/26.49 5/26.83
5 0.0382 0.9748 0.0490 21.2 6/0.02 8/2.63 8/15.66 5/15.88 6/19.80
6 0.0278 0.8240 0.1416 21.1 5/0.08 5/19.80 8/21.59 7/21.87 2/21.97
7 0.1854 0.9571 0.1787 -5.0 5/21.86 6/21.87 1/22.13 2/22.48 8/22.57
8 0.0427 0.9993 0.0530 -5.0 6/2.62 5/2.63 8/15.31 5/15.66 6/21.59
9 0.1787 0.5611 0.2228 -4.7 3/2.91 3/2.90 1/13.36 4/21.16 2/25.02
At this point the structure is obviously solved, and we could use buccaneer or Arp/wArp to add side chains and the rest of the model. 3-fold NCS surely helps!
Could we do better?
Yes, of course (as always). I can think of four things to try:
- an optimization round of running xds for the two datasets
- using a negative offset for STARTING_DOSE in XSCALE.INP, as documented in the XSCALE wiki article.
- use MERGE=TRUE in XDSCONV.INP. I tried it and this gives 20 solutions with CCall+CCweak > 25 out of 1000 trials, whereas MERGE=FALSE (the default) gives only 4 solutions!
- adding the "secondparts" data assuming this is a longer wavelength (but see above for an alternative explanation)
But this time we learn that one has to take special care of the data in particular when they were measured by someone else who does not tell us everything we need to know. Second, zero-dose extrapolation made the day.
Availability of data
The XDS/XSCALE - produced data are available at 1y13-raddam-F.mtz (amplitudes) and 1y13-raddam-I.mtz(intensities). In addition I provide [1] and [2] to enable investigating based on the original XDS_ASCII.HKL files.
Post scriptum
In a discussion with Gerard Bricogne and Clemens Vonrhein after the ACA2011 workshop it turned out that my theory, which claims that E1 and E2 are actually the same wavelength, is wrong. This was investigated by looking at the difference map (obtained using phenix.fobs_minus_fobs_map) of E1 and E2 (taking the first ~370 frames in each case) phased with the 1y13 model, which shows three strong (14-19 sigma) peaks. The fact that the 1-370 pieces merge so well seems to be a consequence of the fact that the anomalous signal of the two wavelengths is so similar, and the dispersive difference between the wavelengths does not significantly decrease the high correlation coefficient in data scaling.
Thus the above describes a pseudo-SAD solution, and even better phasing would be obtained by keeping the wavelengths separate and doing MAD (in fact DAD) - but zero-dose extrapolation could and should be done in the same way. I've therefore continued the analysis in 1Y13-revisited.