Tough Spots ACA2014
There are only 10 frames available to the public at the time of the ACA2014, so we'll see what we can learn from these.
After starting XDSGUI, we go the "Frames" tab and load frame 140. We then move the mouse to the place where the beam stop position is (1584, 1542) because the header values are obviously wrong. These values are then entered into the XDS.INP tab to have
ORGX= 1584.0 ORGY= 1542.0
and adjust
DATA_RANGE=140 149 SPOT_RANGE=140 149
because generate_XDS.INP (which is a script that XDSGUI uses) assumes that frame numbers start at 1. We then "Save" and "Run XDS".
Unfortunately (but not quite unexpectedly, given the poor data), IDXREF stops with an the message:
!!! ERROR !!! INSUFFICIENT PERCENTAGE (< 50%) OF INDEXED REFLECTIONS AUTOMATIC DATA PROCESSING STOPPED. AS THE CRITERIA FOR A GOOD SOLUTION ARE RATHER STRICT, YOU MAY CHOOSE TO CONTINUE DATA PROCESSING AFTER CHANGING THE "JOB="-CARD IN "XDS.INP" TO "JOB= DEFPIX INTEGRATE CORRECT". IF THE BEST SOLUTION IS REALLY NONSENSE YOU SHOULD FIRST HAVE A LOOK AT THE ASCII-FILE "SPOT.XDS". THIS FILE CONTAINS THE INITIAL SPOT LIST SORTED IN DECREASING SPOT INTENSITY. SPOTS NEAR THE END OF THE FILE MAY BE ARTEFACTS THAT CAN BE ERASED. ALTERNATIVELY YOU MAY TRY DIFFERENT VALUES FOR "INDEX_ORIGIN" AS SUGGESTED IN THE ABOVE LISTING. IF THE CRYSTAL HAS SLIPPED AT THE BEGINNING OF DATA COLLECTION YOU MAY CHOOSE TO SKIP SOME OF THE FIRST FRAMES BY CHANGING THE "DATA_RANGE=" IN FILE "XDS.INP" AND START ALL OVER AGAIN.
Upon inspection of IDXREF.LP, we find
# COORDINATES OF REC. BASIS VECTOR LENGTH 1/LENGTH 1 -0.0074106-0.0078746-0.0096180 0.0144717 69.10 2 0.0161275-0.0177932 0.0018581 0.0240862 41.52 3 -0.0063143-0.0049258 0.0088081 0.0119045 84.00 CLUSTER COORDINATES AND INDICES WITH RESPECT TO REC. LATTICE BASIS VECTORS # COORDINATES OF VECTOR CLUSTER FREQUENCY CLUSTER INDICES 1 -0.0160472 0.0177317-0.0019319 437. 0.00 -1.00 -0.01 2 -0.0137156-0.0127408-0.0007731 375. 1.00 -0.00 1.00 3 -0.0297229 0.0049461-0.0025837 345. 0.99 -0.99 1.00 4 -0.0023894 0.0305421-0.0010979 344. -1.00 -1.00 -1.00 5 0.0321961-0.0355153 0.0038075 320. -0.00 2.00 0.01 6 -0.0087489 0.0256212 0.0075593 268. -0.99 -1.00 -0.01 7 0.0074386 0.0078204 0.0094374 256. -0.99 0.00 -0.01 8 0.0223977-0.0127581-0.0067617 251. -0.01 1.00 -0.99 9 0.0459042-0.0228053 0.0045272 250. -1.00 2.00 -1.00 10 0.0248981-0.0434002-0.0058534 247. 0.99 2.00 -0.00 11 -0.0184690 0.0482571-0.0029946 242. -0.99 -1.99 -1.00 12 0.0235478-0.0099933 0.0113274 240. -0.99 1.00 -0.01 13 0.0385187-0.0305663-0.0049896 237. -0.01 2.00 -0.99 14 -0.0063089-0.0049976 0.0085815 229. 0.01 0.00 0.99 15 0.0396875-0.0277897 0.0131522 225. -0.99 2.00 -0.01 ...
So all the difference vectors are integral, which gives us confidence into the primitive cell parameters, listed below the table:
PARAMETERS OF THE REDUCED CELL (ANGSTROEM & DEGREES)
41.52 69.10 84.01 90.28 90.43 90.45
Is it a single lattice?
SUBTREE POPULATION
1 1220
2 33
3 7
4 4
...
Well, almost all (1220) reflections do belong to the prominent lattice.
Next, the program tests alternative origins:
XD,YD computed direct beam position (pixels) on detector
given beam position (pixel): 1584.00 1542.00
X,Y,Z computed coordinates of the direct beam wave vector
DH,DK,DL mean absolute difference between observed and
fitted indices
INDEX_ QUALITY DELTA XD YD X Y Z DH DK DL
ORIGIN
0 0 0 2.8 0.4 1572.6 1549.6 -0.0056 0.0037 0.9992 0.23 0.04 0.05
0 0 -1 7.4 0.5 1585.6 1560.7 0.0008 0.0091 0.9992 0.23 0.43 0.55
0 -1 0 9.4 0.6 1587.8 1564.7 0.0018 0.0111 0.9992 0.23 0.46 0.58
0 0 1 9.4 0.7 1559.8 1538.8 -0.0118 -0.0016 0.9992 0.23 0.39 0.50
0 -1 1 11.6 0.4 1575.0 1553.8 -0.0044 0.0058 0.9992 0.23 0.87 1.10
0 1 -1 12.1 0.4 1570.1 1545.3 -0.0068 0.0016 0.9992 0.23 0.90 1.16
0 1 0 12.3 0.8 1557.1 1534.2 -0.0131 -0.0038 0.9991 0.23 0.49 0.64
1 0 0 13.8 1.0 1605.7 1513.0 0.0106 -0.0141 0.9991 0.23 0.05 0.06
0 -1 -1 15.0 1.1 1600.7 1575.8 0.0082 0.0164 0.9991 0.23 0.06 0.07
...
and based on the given origin, the QUALITY is best and the deviations DH, DK, DL are small - at least for DK and DL, whereas the reflections are smeared along the short axis.
Next, the possible Bravais lattices are tested for consistence with the primitive cell:
LATTICE- BRAVAIS- QUALITY UNIT CELL CONSTANTS (ANGSTROEM & DEGREES) CHARACTER LATTICE OF FIT a b c alpha beta gamma * 44 aP 0.0 41.8 68.9 84.1 90.0 91.1 91.6 * 31 aP 1.3 41.8 68.9 84.1 90.0 88.9 88.4 * 34 mP 20.7 41.8 84.1 68.9 90.0 91.6 91.1 * 33 mP 24.1 41.8 68.9 84.1 90.0 91.1 91.6 * 35 mP 42.2 68.9 41.8 84.1 91.1 90.0 91.6 * 32 oP 43.5 41.8 68.9 84.1 90.0 91.1 91.6 29 mC 239.6 41.8 142.9 84.1 90.4 91.1 74.6 28 mC 244.6 41.8 172.4 68.9 90.4 91.6 77.1 ...
Good "Quality of fit" values (0 to 1) are only obtained for P1 ("aP"), and medium-quality (around 20) for two different settings of P2(1) ("mP"), namely those with the middle and the long axis as unique axes. If the short axis were considered the unique axis, the "Quality of fit" is significantly worse (43.5) so this is not an option. Thus, we've narrowed down the space group possibilities; only three are left.
INTEGRATE and CORRECT
To continue after the error message printed by IDXREF, we change XDS.INP to have
JOB= DEFPIX INTEGRATE CORRECT
and then "Save" and "Run XDS".
The program happily integrates
IMAGE IER SCALE NBKG NOVL NEWALD NSTRONG NREJ SIGMAB SIGMAR 140 0 1.003 8573222 0 5737 187 18 0.1577 0.2374 141 0 1.009 8575812 0 5755 175 7 0.1714 0.2758 142 0 1.008 8584295 0 5754 172 9 0.1604 0.2698 143 0 1.015 8580937 0 5710 160 15 0.1743 0.2532 144 0 1.012 8584356 0 5736 178 12 0.1553 0.2576 145 0 1.012 8588220 0 5760 184 18 0.1676 0.2299 146 0 1.015 8584920 0 5762 151 11 0.1732 0.2858 147 0 1.016 8586552 0 5774 154 13 0.1778 0.3305 148 0 1.017 8583396 0 5765 178 11 0.1638 0.3394 149 0 1.015 8586598 0 5811 154 9 0.1684 0.3231
and then goes to the CORRECT stage.
Unfortunately, the automatic space group determination is difficult, because there are too few symmetry-related reflections.
SPACE-GROUP UNIT CELL CONSTANTS UNIQUE Rmeas COMPARED LATTICE- NUMBER a b c alpha beta gamma CHARACTER
1 41.9 68.7 84.0 90.2 89.0 88.5 182 0.0 0 31 aP
16 41.9 68.7 84.0 90.0 90.0 90.0 165 72.5 17 32 oP
3 68.7 41.9 84.0 90.0 90.2 90.0 168 70.8 14 35 mP
3 41.9 68.7 84.0 90.0 91.0 90.0 180 136.1 2 33 mP
3 41.9 84.0 68.7 90.0 91.5 90.0 181 0.0 1 34 mP
1 41.9 68.7 84.0 90.2 91.0 91.5 182 0.0 0 44 aP
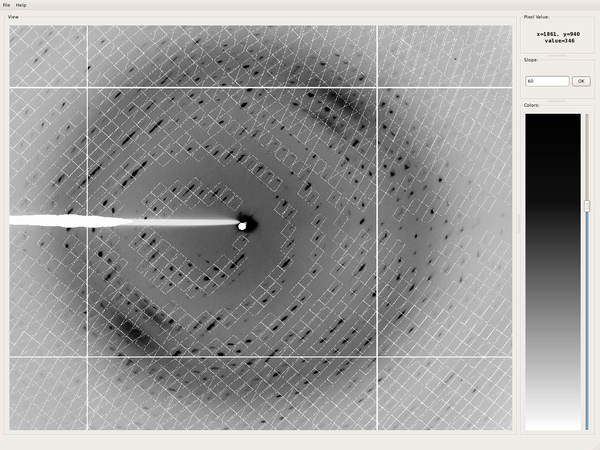
It may be interesting to look at the predicted reflection positions at this stage. So we move to the TOOLS tab and run "Show frame with predicted spots" for frame 140. This gives
The agreement between actual and predicted spots is reasonably good.
At this point, we cannot continue without more information.