1Y13-DAD: Difference between revisions
→SHELC: fix typo |
mNo edit summary |
||
| Line 327: | Line 327: | ||
== Availability of data == | == Availability of data == | ||
The directory [ftp:// | The directory [ftp://{{SERVERNAME}}/pub/xds-datared/1y13] has tarballs of the raw data. The XDS-processed data are available at [ftp://{{SERVERNAME}}/pub/xds-datared/1y13/e1_1-372_XDS_ASCII.HKL.bz2] and [ftp://{{SERVERNAME}}/pub/xds-datared/1y13/e2_1-369_XDS_ASCII.HKL.bz2]. | ||
Revision as of 17:34, 19 December 2019
This is a continuation of 1Y13 investigating how much the pseudo-SAD structure solution performed in that article can be improved by using both wavelengths separately.
Please note that the "second parts" of both E1 and E2 were not used, in order to be more strictly comparable to the analysis as pseudo-SAD done before.
XSCALE using zero-dose extrapolation
This is XSCALE.INP as in 1Y13, but this time using different output files:
UNIT_CELL_CONSTANTS=103.316 103.316 131.456 90.000 90.000 90.000 SPACE_GROUP_NUMBER=96 OUTPUT_FILE=ip.ahkl INPUT_FILE=../e1_1-372/XDS_ASCII.HKL CRYSTAL_NAME=a OUTPUT_FILE=hrem.ahkl INPUT_FILE=../e2_1-369/XDS_ASCII.HKL CRYSTAL_NAME=a
Note the use of "CRYSTAL_NAME=a" for both wavelengths. It might make sense to use different CRYSTAL_NAMEs for different heavy-atom soaks, but in this case clearly the slopes should be the same, and not depend on wavelength.
The output (XSCALE.LP) is ...
...
a b ISa ISa0 INPUT DATA SET
6.090E+00 3.706E-04 21.05 22.37 ../e1_1-372/XDS_ASCII.HKL
5.704E+00 3.823E-04 21.41 22.82 ../e2_1-369/XDS_ASCII.HKL
...
CORRELATION OF COMMON DECAY-FACTORS BETWEEN INPUT DATA SETS
-----------------------------------------------------------
First INPUT_FILE= ../e2_1-369/XDS_ASCII.HKL
CRYSTAL_NAME= a
Second INPUT_FILE= ../e1_1-372/XDS_ASCII.HKL
CRYSTAL_NAME= a
RESOLUTION NUMBER CORRELATION
LIMIT OF PAIRS FACTOR
9.40 211 0.962
6.64 443 0.962
5.43 589 0.937
4.70 695 0.967
4.20 765 0.949
3.84 838 0.934
3.55 810 0.942
3.32 777 0.926
3.13 666 0.888
2.97 559 0.838
2.83 377 0.643
2.71 306 0.810
2.61 211 0.614
2.51 165 0.506
2.43 93 0.326
2.35 134 0.766
2.28 114 0.653
2.21 95 0.748
2.16 86 0.498
2.10 54 0.187
total 7988 0.790
X-RAY DOSE PARAMETERS USED FOR EACH INPUT DATA SET
--------------------------------------------------
CRYSTAL_NAME= a
STARTING_DOSE DOSE_RATE NAME OF INPUT FILE
initial refined initial refined
0.000E+00 9.676E+00 1.000E+00 1.000E+00 ../e1_1-372/XDS_ASCII.HKL
0.000E+00 0.000E+00 1.000E+00 1.027E+00 ../e2_1-369/XDS_ASCII.HKL
STATISTICS OF 0-DOSE CORRECTED DATA FROM EACH CRYSTAL
-----------------------------------------------------
NUNIQUE = Number of unique reflections with enough symmetry-
related observations to determine a decay factor b(h)
N0-DOSE = Number of 0-dose extrapolated unique reflections
NERROR = Number of unique extrapolated reflections expected
to be overfitted. A large ratio of N0-DOSE/NERROR
justifies the data correction as carried out here.
S_corr = mean value of Sigma(I) for 0-dose extrapolated data
S_norm = mean value of Sigma(I) for the same data but
without 0-dose extrapolation.
NFREE = degrees of freedom for calculating S_corr
CRYSTAL_NAME= a
RESOLUTION NUNIQUE N0-DOSE N0-DOSE/ S_corr/ NFREE
LIMIT NERROR S_norm
9.40 498 379 73.8 0.543 3223
6.64 912 701 83.6 0.550 6217
5.43 1143 894 78.3 0.574 8091
4.70 1352 1044 74.8 0.600 9702
4.20 1518 1130 70.4 0.620 10589
3.84 1665 1183 75.3 0.630 11105
3.55 1787 1222 64.8 0.672 11949
3.32 1941 1290 57.9 0.690 12756
3.13 2043 1174 49.6 0.718 11904
2.97 2182 1106 47.7 0.750 11541
2.83 2281 909 40.2 0.798 9640
2.71 2352 817 33.7 0.825 8657
2.61 2467 699 34.2 0.848 7355
2.51 2566 627 31.6 0.875 6576
2.43 2624 505 30.5 0.896 5340
2.35 2709 624 31.8 0.889 6203
2.28 2821 591 29.1 0.893 6032
2.21 2880 557 32.8 0.906 5739
2.16 2959 445 29.7 0.908 4388
2.10 2860 419 29.8 0.926 3804
total 41560 16316 46.9 0.739 160811
******************************************************************************
SCALING FACTORS FOR Sigma(I) AS FUNCTION OF RESOLUTION
******************************************************************************
SCALING FACTORS FOR Sigma(I) FOR DATA SET ../e1_1-372/XDS_ASCII.HKL
RESOLUTION (ANGSTROM)
10.33 6.12 4.76 4.03 3.56 3.23 2.97 2.76 2.60 2.46 2.34 2.23 2.14
FACTOR 0.71 0.81 0.84 0.92 0.99 0.98 0.98 0.98 0.97 0.97 1.09 0.99 0.98
SCALING FACTORS FOR Sigma(I) FOR DATA SET ../e2_1-369/XDS_ASCII.HKL
RESOLUTION (ANGSTROM)
10.32 6.11 4.76 4.03 3.56 3.22 2.97 2.76 2.60 2.46 2.34 2.23 2.14
FACTOR 0.73 0.83 0.85 0.92 1.00 1.00 1.01 1.00 0.99 0.98 1.10 1.01 0.98
...
STATISTICS OF SCALED OUTPUT DATA SET : ip.ahkl
FILE TYPE: XDS_ASCII MERGE=FALSE FRIEDEL'S_LAW=FALSE
279 OUT OF 300965 REFLECTIONS REJECTED
300686 REFLECTIONS ON OUTPUT FILE
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
9.40 3072 832 883 94.2% 1.5% 1.8% 3050 70.26 1.7% 1.0% 90% 2.898 311
6.64 6040 1608 1621 99.2% 1.4% 2.0% 6029 62.36 1.7% 1.1% 84% 2.530 681
5.43 7697 2059 2086 98.7% 1.8% 2.2% 7684 54.05 2.0% 1.4% 80% 2.263 899
4.70 9394 2483 2498 99.4% 1.7% 2.3% 9378 54.17 2.0% 1.3% 68% 1.584 1108
4.20 10574 2793 2821 99.0% 1.8% 2.4% 10559 49.82 2.1% 1.6% 58% 1.414 1261
3.84 11711 3090 3117 99.1% 2.2% 2.7% 11700 42.53 2.6% 2.0% 51% 1.248 1411
3.55 12869 3344 3366 99.3% 2.8% 3.2% 12860 35.46 3.3% 2.6% 36% 1.115 1540
3.32 14042 3626 3653 99.3% 3.4% 3.8% 14037 30.69 3.9% 3.7% 28% 1.071 1678
3.13 15173 3839 3848 99.8% 5.0% 5.3% 15170 23.94 5.8% 5.4% 25% 0.992 1793
2.97 16326 4109 4118 99.8% 7.6% 7.8% 16316 17.71 8.7% 8.7% 20% 0.952 1916
2.83 17243 4308 4320 99.7% 11.0% 11.4% 17229 13.36 12.7% 12.7% 13% 0.905 2014
2.71 17870 4467 4478 99.8% 14.7% 14.9% 17854 10.72 16.9% 15.9% 14% 0.890 2095
2.61 18715 4696 4710 99.7% 22.3% 22.6% 18699 7.40 25.7% 26.1% 9% 0.859 2207
2.51 19552 4884 4896 99.8% 29.6% 30.1% 19535 5.86 34.1% 32.8% 13% 0.856 2298
2.43 20069 5018 5027 99.8% 42.9% 43.9% 20052 4.16 49.5% 49.3% 7% 0.806 2372
2.35 20089 5176 5222 99.1% 59.8% 59.2% 20067 3.07 69.3% 69.4% 20% 0.843 2434
2.28 21137 5378 5423 99.2% 79.1% 82.2% 21120 2.28 91.4% 86.9% 11% 0.745 2536
2.21 21368 5513 5541 99.5% 71.0% 71.6% 21346 2.40 82.2% 78.6% 11% 0.822 2608
2.16 20089 5681 5703 99.6% 91.4% 94.6% 20039 1.75 108.0% 117.6% 4% 0.727 2665
2.10 17656 5567 5912 94.2% 118.8% 119.6% 17377 1.18 142.9% 169.2% 3% 0.703 2467
total 300686 78471 79243 99.0% 4.8% 5.2% 300101 16.79 5.5% 14.9% 23% 1.000 36294
...
STATISTICS OF SCALED OUTPUT DATA SET : hrem.ahkl
FILE TYPE: XDS_ASCII MERGE=FALSE FRIEDEL'S_LAW=FALSE
369 OUT OF 306214 REFLECTIONS REJECTED
305845 REFLECTIONS ON OUTPUT FILE
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
9.40 3069 837 883 94.8% 1.6% 1.9% 3050 68.80 1.8% 1.1% 82% 2.306 313
6.64 6015 1604 1621 99.0% 1.5% 2.0% 6006 60.72 1.8% 1.2% 74% 2.109 680
5.43 7676 2058 2086 98.7% 1.8% 2.2% 7661 52.32 2.1% 1.5% 72% 1.857 898
4.70 9343 2477 2498 99.2% 1.7% 2.3% 9328 52.95 2.0% 1.4% 62% 1.379 1109
4.20 10560 2794 2821 99.0% 1.8% 2.4% 10549 48.56 2.1% 1.6% 55% 1.318 1266
3.84 11644 3086 3117 99.0% 2.3% 2.8% 11630 40.95 2.7% 2.2% 49% 1.178 1406
3.55 12858 3335 3366 99.1% 3.0% 3.4% 12841 33.93 3.5% 2.8% 29% 1.037 1530
3.32 14026 3632 3653 99.4% 3.8% 4.1% 14017 28.81 4.4% 4.2% 27% 1.034 1679
3.13 15126 3841 3848 99.8% 5.6% 5.9% 15120 21.84 6.5% 6.1% 22% 0.944 1791
2.97 16280 4107 4118 99.7% 8.8% 9.0% 16277 15.84 10.2% 10.4% 14% 0.923 1918
2.83 17150 4315 4320 99.9% 12.8% 13.2% 17142 11.76 14.7% 15.1% 13% 0.886 2025
2.71 17781 4468 4478 99.8% 16.9% 17.2% 17763 9.47 19.4% 19.1% 12% 0.875 2092
2.61 18593 4701 4710 99.8% 25.7% 26.2% 18576 6.47 29.6% 30.2% 13% 0.868 2211
2.51 19427 4887 4896 99.8% 33.6% 34.4% 19409 5.14 38.7% 37.4% 12% 0.845 2301
2.43 19936 5008 5027 99.6% 49.0% 50.4% 19920 3.66 56.5% 57.1% 3% 0.758 2368
2.35 19943 5165 5222 98.9% 66.9% 65.8% 19923 2.73 77.6% 78.1% 21% 0.857 2426
2.28 21002 5385 5423 99.3% 90.3% 93.8% 20979 2.01 104.5% 102.5% 10% 0.730 2534
2.21 21621 5522 5541 99.7% 81.5% 82.0% 21600 2.11 94.3% 89.1% 10% 0.801 2614
2.16 22494 5684 5703 99.7% 109.4% 111.6% 22474 1.63 126.4% 125.0% 6% 0.742 2698
2.10 21299 5607 5912 94.8% 140.8% 141.1% 21156 1.21 163.3% 164.3% 6% 0.724 2574
total 305843 78513 79243 99.1% 5.3% 5.8% 305421 15.82 6.1% 16.3% 20% 0.950 36433
hkl2map
SHELXC
SHELXD
Again we use only 3.3A data for the substructure, and have SHELXD look for 3 sites:
This works beautifully and with a high success rate - when treating the data as pseudo-SAD, there was only 1 correct solution out of 100 trials.
SHELXE
has no problem phasing the data:
These are the last lines of the output of SHELXE run from hkl2map:
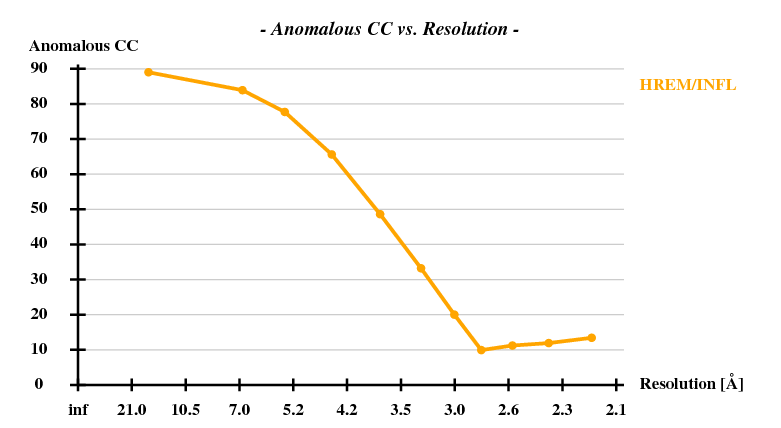
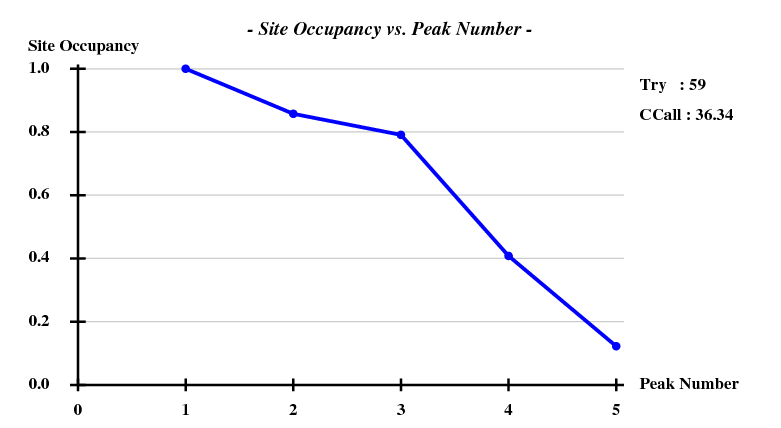
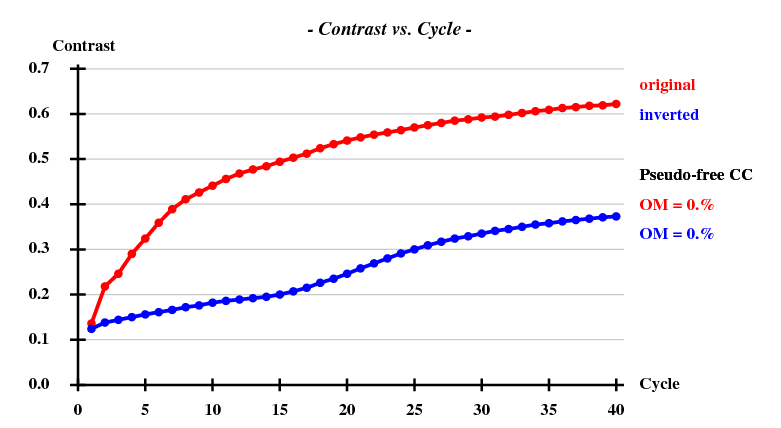
... <wt> = 0.300, Contrast = 0.622, Connect. = 0.775 for dens.mod. cycle 40 Estimated mean FOM and mapCC as a function of resolution d inf - 4.62 - 3.64 - 3.17 - 2.88 - 2.67 - 2.51 - 2.38 - 2.27 - 2.18 - 2.11 <FOM> 0.652 0.674 0.622 0.565 0.511 0.476 0.440 0.440 0.413 0.415 <mapCC> 0.822 0.875 0.853 0.821 0.785 0.755 0.764 0.766 0.698 0.696 N 4207 4230 4223 4138 4187 4208 4292 4410 4320 3702 Estimated mean FOM = 0.521 Pseudo-free CC = 56.08 % Density (in map sigma units) at input heavy atom sites Site x y z occ*Z density 1 0.2269 0.7540 0.1175 34.0000 49.55 2 0.3067 0.4511 0.1298 29.1550 41.44 3 0.0275 0.8228 0.1397 26.8906 37.74 4 0.1805 0.5336 0.2183 13.8686 23.17 5 0.2199 0.7550 0.0807 4.1582 4.40 Site x y z h(sig) near old near new 1 0.2271 0.7550 0.1178 49.8 1/0.11 12/4.93 11/9.01 8/13.52 5/19.89 2 0.3066 0.4517 0.1298 41.6 2/0.07 9/3.05 7/16.26 10/19.04 4/19.40 3 0.0277 0.8231 0.1402 37.8 3/0.08 11/18.31 7/18.33 6/19.52 8/21.52 4 0.1795 0.5337 0.2173 23.5 4/0.17 10/2.84 7/14.74 5/15.55 9/17.53 5 0.1570 0.6337 0.3039 11.6 4/15.48 4/15.55 10/16.93 8/18.43 1/19.89 6 0.0384 0.9752 0.0526 8.8 3/19.51 6/16.61 7/19.04 3/19.52 8/22.99
At this point, I copied the "dad.hat" file with its updated substructure (which has all 6 sites) to "dad_fa.res", thus overwriting the coordinates found by SHELXD (which has 4 correct, and one wrong sites). Then I used the beta version with the same command as in 1Y13:
shelxe.beta -a -q -h6 -b -s0.585 -m40 -n3 dad dad_fa
indeed giving 3 chains with around 155 residues, each
... 0 groups of atoms closer than 2.4A (e.g. disulfides) fused together for NCS 3-fold NCS found, mode 2, mean deviation for all 6 input atoms = 0.142 A Overall CC between Eobs (from delF) and Ecalc (from heavy atoms) = 12.58% ... ... Applying NCS and splicing-in transformed chains that fit density 465 residues left after pruning, divided into chains as follows: A: 150 B: 159 C: 156 CC for partial structure against native data = 42.18 % ... <wt> = 0.300, Contrast = 0.825, Connect. = 0.821 for dens.mod. cycle 40 Estimated mean FOM and mapCC as a function of resolution d inf - 4.62 - 3.64 - 3.17 - 2.88 - 2.67 - 2.51 - 2.38 - 2.27 - 2.18 - 2.11 <FOM> 0.726 0.756 0.753 0.717 0.696 0.688 0.632 0.614 0.598 0.557 <mapCC> 0.846 0.898 0.932 0.930 0.921 0.929 0.931 0.925 0.889 0.873 N 4207 4230 4223 4138 4187 4208 4292 4410 4320 3702 Estimated mean FOM = 0.675 Pseudo-free CC = 71.89 % Density (in map sigma units) at input heavy atom sites Site x y z occ*Z density 1 0.2271 0.7550 0.1178 34.0000 42.57 2 0.3066 0.4517 0.1298 28.3968 33.06 3 0.0277 0.8231 0.1402 25.8264 31.03 4 0.1795 0.5337 0.2173 16.0412 24.69 5 0.1570 0.6337 0.3039 7.9390 22.32 6 0.0384 0.9752 0.0526 6.0078 14.61 Site x y z h(sig) near old near new 1 0.2276 0.7565 0.1184 42.8 1/0.18 7/2.75 8/3.22 5/19.63 3/21.97 2 0.3065 0.4527 0.1293 33.2 2/0.12 4/19.49 6/26.72 6/28.46 8/30.50 3 0.0278 0.8234 0.1410 31.1 3/0.10 6/19.75 8/21.21 1/21.97 7/23.88 4 0.1774 0.5342 0.2164 25.4 4/0.25 5/15.68 2/19.49 8/24.15 1/26.84 5 0.1573 0.6343 0.3046 22.5 5/0.11 4/15.68 7/18.33 1/19.63 8/22.10 6 0.0382 0.9754 0.0502 15.3 6/0.31 6/16.07 3/19.75 2/26.72 2/28.46 7 0.2484 0.7678 0.1089 -5.5 1/2.82 1/2.75 8/5.73 5/18.33 3/23.88 8 0.2095 0.7314 0.1210 -5.3 1/3.07 1/3.22 7/5.73 3/21.21 5/22.10
What do we learn?
In no particular order:
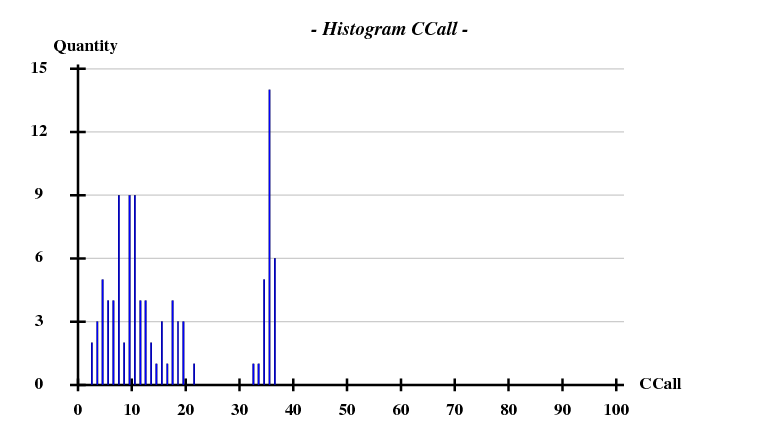
- That the dispersive signal helps a lot in substructure solution: 27 successful trial in 100 using DAD, instead of 1 using pseudo-SAD.
- That the correlation coefficient between two wavelengths of a MAD experiment can be better than 0.9995 if there is no difference in radiation damage (in other words, the dispersive signal does not seem to significantly lower the correlation).
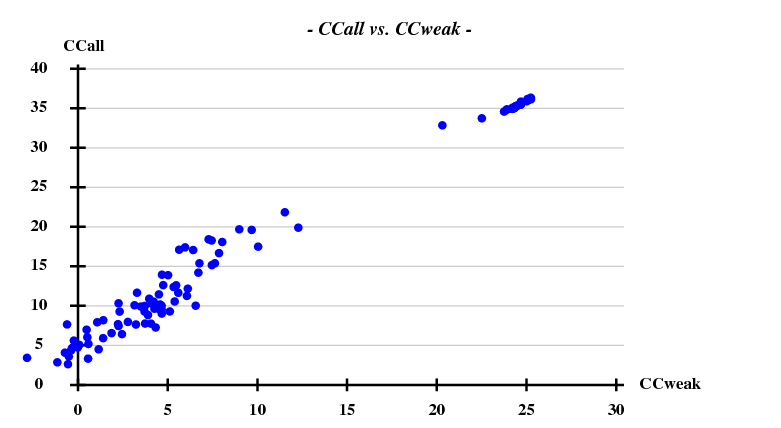
- That zero-dose extrapolation helps a lot, and works very well: if it is not done, we obtain only 5 correct solutions out of 100, and the highest CCall / CCweak is 17.85 / 12.33 instead of 36.34 / 25.24 (I don't show the plots here).
- That the wavelength change only takes 3 seconds at this beamline, which makes such an experiment really attractive.
Availability of data
The directory [1] has tarballs of the raw data. The XDS-processed data are available at [2] and [3].