Simulated-1g1c: Difference between revisions
No edit summary |
mNo edit summary |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 530: | Line 530: | ||
but there does not appear a "magic bullet" that would produce much better data than with the quick bootstrap approach. | but there does not appear a "magic bullet" that would produce much better data than with the quick bootstrap approach. | ||
== | == Trying to solve the structure == | ||
First, we repeat xscale after inserting FRIEDEL'S_LAW=FALSE into XSCALE.INP . This gives us | First, we repeat xscale after inserting FRIEDEL'S_LAW=FALSE into XSCALE.INP . This gives us | ||
| Line 562: | Line 562: | ||
One hint towards the contents of the "crystal" is that the information about the simulated data contained the strings "1g1c". This structure | One hint towards the contents of the "crystal" is that the information about the simulated data contained the strings "1g1c". This structure (spacegroup 19, cell axes 38.3, 78.6, 79.6) is available from the PDB; it contains 2 chains of 99 residues, and a chain has 2 Cys and 2 Met. Thus we assume that the simulated data may represent SeMet-SAD. Using [[ccp4:hkl2map|hkl2map]], we can easily find four sites with good CCall/CCweak: | ||
[[File:Simulated-1g1c-ccall-ccweak2.png]] | [[File:Simulated-1g1c-ccall-ccweak2.png]] | ||
| Line 573: | Line 573: | ||
shelxe.beta -m40 -a -q -h -s0.54 -b -i -e -n 1g1c 1g1c_fa | shelxe.beta -m40 -a -q -h -s0.54 -b -i -e -n 1g1c 1g1c_fa | ||
but it traces only about 62 residues. The density looks reasonable, though. | but it traces only about 62 residues. The density looks somewhat reasonable, though. | ||
The files [ | The files [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-I.mtz xds-simulated-1g1c-I.mtz] and [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-F.mtz xds-simulated-1g1c-F.mtz] are available. | ||
I refined against 1g1c.pdb: | |||
phenix.refine xds-simulated-1g1c-F.mtz 1g1c.pdb refinement.input.xray_data.r_free_flags.generate=True | |||
The result was | |||
Start R-work = 0.3453, R-free = 0.3501 | |||
Final R-work = 0.2170, R-free = 0.2596 | |||
which appears reasonable. | |||
== Notes == | |||
=== Towards better completeness: using the first two frames instead of only the first === | |||
We might want better (anomalous) completeness than what is given by only the very first frame of each dataset. To this end, we change in the XDS.INP part of our script : | |||
DATA_RANGE=1 2 | |||
then run the script which reduces the 100 datasets. When this has finished, we insert in XSCALE.INP | |||
NBATCH=2 | |||
after each INPUT_FILE line (this can be easily done using <pre> awk '{print $0;print "NBATCH=2"}' XSCALE.INP > x </pre>). The reason for this is that by default, XSCALE establishes scalefactors every 5 degrees, but here we want scalefactors for every frame, because the radiation damage is so strong. This gives: | |||
NOTE: Friedel pairs are treated as different reflections. | |||
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION | |||
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano | |||
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr | |||
8.05 1922 467 476 98.1% 4.2% 6.6% 1888 20.04 4.8% 2.8% 84% 1.887 142 | |||
5.69 3494 864 882 98.0% 4.5% 6.8% 3429 18.67 5.2% 3.1% 83% 1.635 297 | |||
4.65 4480 1111 1136 97.8% 5.3% 6.7% 4395 18.89 6.1% 3.5% 66% 1.347 406 | |||
4.03 5197 1325 1357 97.6% 6.2% 6.8% 5101 18.37 7.1% 4.3% 43% 1.156 499 | |||
3.60 5916 1500 1533 97.8% 6.9% 7.1% 5804 17.83 8.0% 4.7% 36% 1.083 572 | |||
3.29 6601 1657 1694 97.8% 7.6% 7.3% 6476 17.26 8.7% 4.9% 24% 1.029 634 | |||
3.04 7081 1789 1830 97.8% 9.1% 8.0% 6949 15.50 10.4% 6.4% 17% 1.011 693 | |||
2.85 7684 1946 1979 98.3% 10.9% 9.9% 7530 12.95 12.5% 8.1% 16% 0.950 751 | |||
2.68 8101 2062 2100 98.2% 13.1% 12.1% 7935 11.18 15.0% 10.5% 10% 0.888 795 | |||
2.55 8355 2156 2201 98.0% 15.2% 14.9% 8182 9.69 17.5% 12.3% 6% 0.867 837 | |||
2.43 9195 2327 2376 97.9% 18.2% 18.6% 9003 8.20 20.8% 15.4% 6% 0.837 904 | |||
2.32 9495 2377 2428 97.9% 21.3% 21.9% 9304 7.42 24.4% 18.4% 6% 0.800 934 | |||
2.23 9939 2499 2551 98.0% 23.0% 23.3% 9753 7.13 26.4% 19.0% 4% 0.818 987 | |||
2.15 10219 2577 2622 98.3% 25.4% 25.9% 9992 6.63 29.1% 20.6% 1% 0.797 998 | |||
2.08 10712 2704 2766 97.8% 29.4% 30.8% 10508 5.80 33.8% 25.1% 4% 0.793 1071 | |||
2.01 10900 2778 2839 97.9% 30.8% 31.2% 10649 5.50 35.3% 26.2% 4% 0.828 1060 | |||
1.95 11361 2878 2937 98.0% 36.7% 38.2% 11134 4.71 42.1% 31.5% 1% 0.768 1136 | |||
1.90 11641 2943 3000 98.1% 42.7% 45.1% 11405 4.12 49.1% 38.7% -1% 0.775 1165 | |||
1.85 12028 3069 3123 98.3% 54.0% 60.4% 11760 3.19 62.1% 47.5% 5% 0.735 1196 | |||
1.80 11506 3003 3173 94.6% 62.1% 70.6% 11229 2.72 71.6% 60.6% -2% 0.709 1148 | |||
total 165827 42032 43003 97.7% 12.8% 13.3% 162426 8.79 14.7% 15.7% 15% 0.881 16225 | |||
showing that the anomalous completeness, and even the quality of the anomalous signal, can indeed be increased. I doubt, however, that going to three or more frames would improve things even more. | |||
The MTZ files are at [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-F-2frames.mtz] and [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-I-2frames.mtz], respectively. They were of course obtained with XDSCONV.INP: | |||
INPUT_FILE=temp.ahkl | |||
OUTPUT_FILE=temp.hkl CCP4_I | |||
for the intensities, and | |||
INPUT_FILE=temp.ahkl | |||
OUTPUT_FILE=temp.hkl CCP4 | |||
for the amplitudes. In both cases, after xdsconv we have to run | |||
<pre> | |||
f2mtz HKLOUT temp.mtz<F2MTZ.INP | |||
cad HKLIN1 temp.mtz HKLOUT output_file_name.mtz<<EOF | |||
LABIN FILE 1 ALL | |||
END | |||
EOF | |||
</pre> | |||
Using the default (see above) phenix.refine job, I obtain against the [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-F-2frames.mtz MTZ file with amplitudes]: | |||
Start R-work = 0.3434, R-free = 0.3540 | |||
Final R-work = 0.2209, R-free = 0.2479 | |||
and against the [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-I-2frames.mtz MTZ file with intensities] | |||
Start R-work = 0.3492, R-free = 0.3606 | |||
Final R-work = 0.2244, R-free = 0.2504 | |||
so: '''better R-free is obtained from better data.''' | |||
The statistics from SHELXD and SHELXE don't look better - they were already quite good with a single frame per dataset. The statistics printed by SHELXE (for the correct hand) are: | |||
... | |||
<wt> = 0.300, Contrast = 0.591, Connect. = 0.740 for dens.mod. cycle 50 | |||
Estimated mean FOM and mapCC as a function of resolution | |||
d inf - 3.98 - 3.13 - 2.72 - 2.47 - 2.29 - 2.15 - 2.04 - 1.95 - 1.87 - 1.81 | |||
<FOM> 0.601 0.606 0.590 0.570 0.538 0.542 0.521 0.509 0.529 0.498 | |||
<mapCC> 0.841 0.813 0.811 0.786 0.763 0.744 0.727 0.740 0.761 0.722 | |||
N 2289 2303 2334 2245 2289 2330 2299 2297 2429 2046 | |||
Estimated mean FOM = 0.551 Pseudo-free CC = 59.42 % | |||
... | |||
Site x y z h(sig) near old near new | |||
1 0.7375 0.6996 0.1537 20.4 1/0.06 2/15.05 6/21.38 3/21.54 5/22.03 | |||
2 0.7676 0.7231 0.3419 18.8 3/0.13 5/12.15 1/15.05 3/21.34 4/22.43 | |||
3 0.5967 0.4904 -0.0067 17.2 4/0.10 4/4.90 6/4.94 2/21.34 1/21.54 | |||
4 0.5269 0.5194 -0.0498 17.1 2/0.05 3/4.90 6/7.85 2/22.43 1/22.96 | |||
5 0.4857 0.6896 0.4039 -4.8 3/12.04 2/12.15 1/22.03 3/22.55 2/22.85 | |||
6 0.5158 0.4788 0.0406 4.7 5/1.45 3/4.94 4/7.85 1/21.38 5/23.30 | |||
=== Why this is difficult to solve with SAD phasing === | |||
In the original publication ("Structural evidence for a possible role of reversible disulphide bridge formation in the elasticity of the muscle protein titin" Mayans, O., Wuerges, J., Canela, S., Gautel, M., Wilmanns, M. (2001) Structure 9: 331-340 ) we read: | |||
"This crystal form contains two molecules in the asymmetric unit. They are related by a noncrystallographic two-fold axis, parallel to the crystallographic b axis, located at X = 0.25 and Z = 0.23. This arrangement results in a peak in the native Patterson map at U = 0.5, V = 0, W = 0.47 of peak height 26 σ (42% of the origin peak)." | |||
Unfortunately, the arrangement of substructure sites has (pseudo-)translational symmetry, and may be related to a centrosymmetric arrangement. Indeed, the original structure was solved using molecular replacement. | |||
Using the four sites as given by SHELXE (and default parameters otherwise), I obtained from the [http://cci.lbl.gov/cctbx/phase_o_phrenia.html cctbx - Phase-O-Phrenia server] the following | |||
Plot of relative peak heights: | |||
|* | |||
|* | |||
|* | |||
|* | |||
|** | |||
|** | |||
|*** | |||
|**** | |||
|****** | |||
|************ | |||
|******************** | |||
|***************************** | |||
|********************************* | |||
|*************************************** | |||
|************************************************ | |||
|************************************************************ | |||
|************************************************************ | |||
|************************************************************ | |||
|************************************************************ | |||
|************************************************************ | |||
------------------------------------------------------------- | |||
Peak list: | |||
Relative | |||
height Fractional coordinates | |||
97.8 0.01982 0.49860 -0.00250 | |||
80.2 0.17362 0.71758 0.83714 | |||
71.5 0.02405 0.53538 0.48365 | |||
63.9 -0.00511 0.07044 0.50289 | |||
62.1 0.02410 0.94827 0.48807 | |||
61.3 0.16922 0.28605 0.15985 | |||
56.3 0.12047 0.50910 0.43665 | |||
55.9 0.21871 0.26331 0.30008 | |||
55.7 0.10931 0.47245 0.53659 | |||
53.0 0.22211 0.23746 0.39503 | |||
52.9 0.03449 -0.00661 0.98264 <------ this peak is close to the origin | |||
52.5 0.06905 0.02372 0.05632 <------ this one, too | |||
... | |||
so the strongest peak corresponds to the translation of molecules (0,0.5,0) but the origin peak is at 1/2 of that size, which appears significant. | |||
=== Finally solving the structure === | |||
After thinking about the most likely way that James Holton used to produce the simulated data, I hypothesized that within each frame, the radiation damage is most likely constant, and that there is a jump in radiation damage from frame 1 to 2. Unfortunately for this scenario, the scaling algorithm in CORRECT and XSCALE was changed for the version of Dec-2010, such that it produces best results when the changes are smooth. Therefore, I tried the penultimate version (May-2010) of XSCALE - and indeed that gives significantly better results: | |||
NOTE: Friedel pairs are treated as different reflections. | |||
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION | |||
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano | |||
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr | |||
8.05 1922 467 476 98.1% 4.0% 5.8% 1888 22.37 4.5% 2.5% 84% 1.952 142 | |||
5.69 3494 864 882 98.0% 4.7% 6.0% 3429 20.85 5.4% 3.2% 77% 1.707 297 | |||
4.65 4480 1111 1136 97.8% 5.1% 5.9% 4395 21.13 5.8% 3.3% 68% 1.518 406 | |||
4.03 5197 1325 1357 97.6% 5.3% 6.0% 5101 20.57 6.1% 3.8% 48% 1.280 499 | |||
3.60 5915 1500 1533 97.8% 6.0% 6.3% 5803 19.99 6.9% 4.1% 41% 1.169 572 | |||
3.29 6601 1657 1694 97.8% 6.5% 6.5% 6476 19.42 7.5% 4.6% 27% 1.066 634 | |||
3.04 7080 1789 1830 97.8% 7.6% 7.2% 6948 17.50 8.7% 5.4% 23% 1.037 693 | |||
2.85 7682 1945 1979 98.3% 8.8% 9.0% 7528 14.75 10.1% 7.0% 15% 0.935 750 | |||
2.68 8099 2062 2100 98.2% 11.0% 11.1% 7933 12.81 12.7% 9.1% 13% 0.881 795 | |||
2.55 8351 2155 2201 97.9% 13.3% 13.7% 8178 11.16 15.4% 11.0% 12% 0.872 836 | |||
2.43 9195 2327 2376 97.9% 16.5% 17.2% 9003 9.49 19.0% 15.1% 8% 0.838 904 | |||
2.32 9495 2377 2428 97.9% 19.8% 20.3% 9304 8.62 22.7% 17.3% 4% 0.818 934 | |||
2.23 9936 2498 2551 97.9% 20.8% 21.7% 9751 8.30 23.9% 17.5% 4% 0.830 987 | |||
2.15 10217 2577 2622 98.3% 23.3% 24.0% 9990 7.74 26.7% 19.2% 4% 0.814 998 | |||
2.08 10710 2704 2766 97.8% 27.1% 28.6% 10506 6.82 31.1% 23.5% 5% 0.812 1071 | |||
2.01 10899 2777 2839 97.8% 28.1% 29.2% 10648 6.46 32.3% 25.0% 6% 0.813 1059 | |||
1.95 11361 2878 2937 98.0% 34.4% 35.5% 11134 5.55 39.5% 30.3% 3% 0.780 1136 | |||
1.90 11639 2941 3000 98.0% 40.5% 41.5% 11403 4.88 46.6% 35.9% 0% 0.787 1163 | |||
1.85 12020 3068 3123 98.2% 52.2% 55.1% 11752 3.79 60.0% 47.4% 6% 0.775 1195 | |||
1.80 11506 3003 3173 94.6% 60.8% 64.8% 11229 3.23 70.1% 58.8% 0% 0.765 1148 | |||
total 165799 42025 43003 97.7% 11.7% 12.3% 162399 10.07 13.5% 14.8% 17% 0.908 16219 | |||
Using these data (stored in [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xscale.oldversion]), I was finally able to solve the structure (see screenshot below) - SHELXE traced 160 out of 198 residues. All files produced by SHELXE are in [https://{{SERVERNAME}}/pub/xds-datared/1g1c/shelx]. | |||
[[File:1g1c-shelxe.png]] | |||
It is worth mentioning that James Holton confirmed that my hypothesis is true; he also says that this approach is a good approximation for a multi-pass data collection. | |||
However, generally (i.e. for real data) the smooth scaling (which also applies to absorption correction and detector modulation) gives better results than the previous method of assigning the same scale factor to all reflections of a frame; in particular, it correctly treats those reflections near the border of two frames. | |||
Phenix.refine against these data gives: | |||
Start R-work = 0.3449, R-free = 0.3560 | |||
Final R-work = 0.2194, R-free = 0.2469 | |||
which is only 0.15%/0.10% better in R-work/R-free than the previous best result (see above). | |||
This example shows that it is important to | |||
* have the best data available if a structure is difficult to solve | |||
* know the options (programs, algorithms) | |||
* know as much as possible about the experiment | |||
Latest revision as of 14:14, 24 March 2020
This is an exercise, devised by James Holton, which deals with merging of datasets that were obtained in the presence of strong radiation damage.
The datasets were actually simulated using his program MLFSOM. There are 100 of them, and they are in random orientations wrt each other. Each dataset consists of 15 frames of 1 degree rotation.
The goal of data processing is to obtain a good and complete dataset. In this case, it is tempting to think about the possibility of only using the first frame of each dataset. This has three advantages:
- radiation damage does not lower the resolution
- the completeness should be adequate if the symmetry is at least orthorhombic
- a successful procedure could also serve for processing data from a X-ray Free Electron Laser (see the recent Nature paper at [1])
Preparation
From visual inspection (using adxv) we realize that the first frame of each dataset looks good (diffraction to 2 A), the last bad (10 A), and there is an obvious degradation from each frame to the next.
We have to get some idea about possible spacegroups first. This means processing some of the datasets. Let's choose "xtal100", the last one.
generate_XDS.INP "../../Illuin/microfocus/xtal100_1_0??.img"
To maximize the number of reflections that should be used for spacegroup determination, the only changes to XDS.INP are:
TEST_RESOLUTION_RANGE= 50 0 ! default is 10 4 ; we want all reflections instead
DATA_RANGE= 1 1 ! R-factors involving more than 1 frame are meaningless
! with such strong radiation damage
We run "xds" and, after a few seconds, can inspect IDXREF.LP and CORRECT.LP. It turns out that the primitve cell is 38.3, 79.2, 79.2, 90, 90, 90 which is compatible with tetragonal spacegroups, or those with lower symmetry:
LATTICE- BRAVAIS- QUALITY UNIT CELL CONSTANTS (ANGSTROEM & DEGREES) REINDEXING TRANSFORMATION CHARACTER LATTICE OF FIT a b c alpha beta gamma * 31 aP 0.0 38.3 79.2 79.2 90.0 90.0 90.0 1 0 0 0 0 1 0 0 0 0 1 0 * 44 aP 0.1 38.3 79.2 79.2 90.0 90.0 90.0 -1 0 0 0 0 -1 0 0 0 0 1 0 * 35 mP 0.4 79.2 38.3 79.2 90.0 90.0 90.0 0 1 0 0 1 0 0 0 0 0 -1 0 * 33 mP 0.9 38.3 79.2 79.2 90.0 90.0 90.0 -1 0 0 0 0 -1 0 0 0 0 1 0 * 34 mP 1.1 38.3 79.2 79.2 90.0 90.0 90.0 1 0 0 0 0 0 -1 0 0 1 0 0 * 32 oP 1.2 38.3 79.2 79.2 90.0 90.0 90.0 -1 0 0 0 0 -1 0 0 0 0 1 0 * 20 mC 1.2 112.0 111.9 38.3 90.0 90.0 90.0 0 1 1 0 0 1 -1 0 -1 0 0 0 * 23 oC 1.4 111.9 112.0 38.3 90.0 90.0 90.0 0 -1 1 0 0 1 1 0 -1 0 0 0 * 25 mC 1.4 111.9 112.0 38.3 90.0 90.0 90.0 0 -1 1 0 0 1 1 0 -1 0 0 0 * 21 tP 2.2 79.2 79.2 38.3 90.0 90.0 90.0 0 -1 0 0 0 0 1 0 -1 0 0 0 37 mC 249.8 162.9 38.3 79.2 90.0 90.0 76.4 -1 0 2 0 -1 0 0 0 0 -1 0 0
This table exists in both IDXREF.LP and CORRECT.LP. The next table in CORRECT.LP tells us the Rmeas of the starred (*) lattices:
SPACE-GROUP UNIT CELL CONSTANTS UNIQUE Rmeas COMPARED LATTICE-
NUMBER a b c alpha beta gamma CHARACTER
5 112.0 111.9 38.3 90.0 90.0 90.0 973 0.0 0 20 mC
75 79.2 79.2 38.3 90.0 90.0 90.0 961 93.5 12 21 tP
89 79.2 79.2 38.3 90.0 90.0 90.0 946 30.9 27 21 tP
21 111.9 112.0 38.3 90.0 90.0 90.0 965 31.6 8 23 oC
5 111.9 112.0 38.3 90.0 90.0 90.0 970 77.9 3 25 mC
1 38.3 79.2 79.2 90.0 90.0 90.0 973 0.0 0 31 aP
16 38.3 79.2 79.2 90.0 90.0 90.0 954 6.8 19 32 oP
3 79.2 38.3 79.2 90.0 90.0 90.0 968 5.4 5 35 mP
3 38.3 79.2 79.2 90.0 90.0 90.0 966 5.2 7 33 mP
3 38.3 79.2 79.2 90.0 90.0 90.0 966 10.7 7 34 mP
1 38.3 79.2 79.2 90.0 90.0 90.0 973 0.0 0 44 aP
Obviously the tetragonal lattices seem unfavourable, whereas orthorhombic is good. We repeat this procedure with a few other datasets, and observe that the "orthorhombic hypothesis" is confirmed. E.g. with xtal001 we obtain:
SPACE-GROUP UNIT CELL CONSTANTS UNIQUE Rmeas COMPARED LATTICE-
NUMBER a b c alpha beta gamma CHARACTER
5 111.9 111.9 38.3 90.0 90.0 90.0 939 119.8 5 20 mC
75 79.1 79.1 38.3 90.0 90.0 90.0 939 47.0 5 21 tP
89 79.1 79.1 38.3 90.0 90.0 90.0 865 21.6 79 21 tP
21 111.9 111.9 38.3 90.0 90.0 90.0 939 119.8 5 23 oC
5 111.9 111.9 38.3 90.0 90.0 90.0 939 119.8 5 25 mC
1 38.3 79.1 79.1 90.0 90.0 90.0 944 0.0 0 31 aP
16 38.3 79.1 79.1 90.0 90.0 90.0 875 6.3 69 32 oP
3 79.1 38.3 79.1 90.0 90.0 90.0 944 0.0 0 35 mP
3 38.3 79.1 79.1 90.0 90.0 90.0 875 6.3 69 33 mP
3 38.3 79.1 79.1 90.0 90.0 90.0 944 0.0 0 34 mP
1 38.3 79.1 79.1 90.0 90.0 90.0 944 0.0 0 44 aP
devising a bootstrap procedure
We have to realize that, since the b and c axes are equal, we can index each dataset in two non-equivalent ways. This is the same situation as occurs e.g. for spacegroups P3(x) and P4(x), and means that we'll have to use a REFERENCE_DATA_SET to get the right setting for each of the 100 datasets.
However, we cannot expect that all of the datasets have enough reflections in common with a given dataset. Thus, we have to update and enlarge the REFERENCE_DATA_SET after the first round, using those datasets that have reflections in common with the old REFERENCE_DATA_SET. Then in a second round, we can hopefully identify the correct setting for all datasets. After that, we can scale everything together.
first round of bootstrap
We choose xtal100 as the first reference, and move its XDS_ASCII.HKL to bootstrap/reference.ahkl. A script that goes through all datasets, produces XDS.INP, and runs xds is the following (note that we only REFINE(IDXREF)= ORIENTATION BEAM , and the same for REFINE(INTEGRATE), since it may be useful to keep the b and c axis exactly the same):
#!/bin/csh -f
foreach f ( Illuin/microfocus/xtal*_1_001.img )
setenv x `echo $f | cut -c 19-25`
echo processing $x
rm -rf bootstrap/$x
mkdir bootstrap/$x
cd bootstrap/$x
cat>XDS.INP<<EOF
JOB= XYCORR INIT COLSPOT IDXREF DEFPIX INTEGRATE CORRECT
ORGX= 1511.2 ORGY= 1553.1 ! ORGX=1507 ORGY=1570 if BEAM is not refined
DETECTOR_DISTANCE= 250
OSCILLATION_RANGE= 1
X-RAY_WAVELENGTH= 0.979338
NAME_TEMPLATE_OF_DATA_FRAMES=../../Illuin/microfocus/${x}_1_0??.img
DATA_RANGE=1 1
SPOT_RANGE=1 1
REFERENCE_DATA_SET=../reference.ahkl
TEST_RESOLUTION_RANGE= 50.0 2.0 ! for correlating with reference
SPACE_GROUP_NUMBER=16 ! 0 if unknown
UNIT_CELL_CONSTANTS= 38.3 79.1 79.1 90 90 90 ! mean of CORRECT outputs
INCLUDE_RESOLUTION_RANGE=60 1.8 ! after CORRECT, insert high resol limit; re-run CORRECT
TRUSTED_REGION=0.00 1. ! partially use corners of detectors; 1.41421=full use
VALUE_RANGE_FOR_TRUSTED_DETECTOR_PIXELS=7000. 30000. ! often 8000 is ok
MINIMUM_ZETA=0.05 ! integrate close to the Lorentz zone; 0.15 is default
STRONG_PIXEL=5
MINIMUM_NUMBER_OF_PIXELS_IN_A_SPOT=3 ! default of 6 is sometimes too high
REFINE(INTEGRATE)= ORIENTATION BEAM ! AXIS DISTANCE CELL
REFINE(IDXREF)= ORIENTATION BEAM ! AXIS DISTANCE CELL
! parameters specifically for this detector and beamline:
DETECTOR= ADSC MINIMUM_VALID_PIXEL_VALUE= 1 OVERLOAD= 65000
NX= 3072 NY= 3072 QX= 0.102539 QY= 0.102539 ! to make CORRECT happy if frames are unavailable
DIRECTION_OF_DETECTOR_X-AXIS=1 0 0
DIRECTION_OF_DETECTOR_Y-AXIS=0 1 0
INCIDENT_BEAM_DIRECTION=0 0 1 ! 0.00203 -0.0065 1.02107 ! mean of CORRECT outputs
ROTATION_AXIS=1 0 0 ! at e.g. SERCAT ID-22 this needs to be -1 0 0
FRACTION_OF_POLARIZATION=0.98 ! better value is provided by beamline staff!
POLARIZATION_PLANE_NORMAL=0 1 0
EOF
xds >& xds.log &
sleep 1
cd ../..
end
Running this script takes 2 minutes. After this, it's a good idea to check whether the cell parameters are really what we assumed they are:
grep UNIT_CELL_CO xtal0[01]*/XDS_ASCII.HKL | cut -c24- > CELLPARM.INP cellparm cat CELLPARM.LP
and obtain:
A B C ALPHA BETA GAMMA WEIGHT 38.311 79.096 79.107 90.000 90.000 90.000 1.0 38.292 79.081 79.078 90.000 90.000 90.000 1.0 38.285 79.021 79.048 90.000 90.000 90.000 1.0 38.308 79.106 79.099 90.000 90.000 90.000 1.0 38.298 79.096 79.084 90.000 90.000 90.000 1.0 38.310 79.117 79.109 90.000 90.000 90.000 1.0 38.317 79.120 79.124 90.000 90.000 90.000 1.0 38.302 79.102 79.097 90.000 90.000 90.000 1.0 38.309 79.119 79.134 90.000 90.000 90.000 1.0 38.288 79.098 79.128 90.000 90.000 90.000 1.0 38.294 79.102 79.119 90.000 90.000 90.000 1.0 38.299 79.104 79.100 90.000 90.000 90.000 1.0 38.296 79.113 79.058 90.000 90.000 90.000 1.0 38.322 79.091 79.120 90.000 90.000 90.000 1.0 38.284 79.082 79.094 90.000 90.000 90.000 1.0 38.284 79.103 79.098 90.000 90.000 90.000 1.0 38.303 79.109 79.111 90.000 90.000 90.000 1.0 38.293 79.084 79.083 90.000 90.000 90.000 1.0 38.300 79.095 79.101 90.000 90.000 90.000 1.0
38.300 79.097 79.100 90.000 90.000 90.000 19.0
Why not use all datasets? The reason is that cellparm has a limit of 20 datasets! But it seems to confirm that the cell axes are really 38.3, 79.1, 79.1.
Now we run xscale with the following XSCALE.INP :
OUTPUT_FILE=temp.ahkl INPUT_FILE=../xtal001/XDS_ASCII.HKL INPUT_FILE=../xtal002/XDS_ASCII.HKL INPUT_FILE=../xtal003/XDS_ASCII.HKL INPUT_FILE=../xtal004/XDS_ASCII.HKL INPUT_FILE=../xtal005/XDS_ASCII.HKL INPUT_FILE=../xtal006/XDS_ASCII.HKL INPUT_FILE=../xtal007/XDS_ASCII.HKL INPUT_FILE=../xtal008/XDS_ASCII.HKL INPUT_FILE=../xtal009/XDS_ASCII.HKL INPUT_FILE=../xtal010/XDS_ASCII.HKL INPUT_FILE=../xtal011/XDS_ASCII.HKL INPUT_FILE=../xtal012/XDS_ASCII.HKL INPUT_FILE=../xtal013/XDS_ASCII.HKL INPUT_FILE=../xtal014/XDS_ASCII.HKL INPUT_FILE=../xtal015/XDS_ASCII.HKL INPUT_FILE=../xtal016/XDS_ASCII.HKL INPUT_FILE=../xtal017/XDS_ASCII.HKL INPUT_FILE=../xtal018/XDS_ASCII.HKL INPUT_FILE=../xtal019/XDS_ASCII.HKL INPUT_FILE=../xtal020/XDS_ASCII.HKL INPUT_FILE=../xtal021/XDS_ASCII.HKL INPUT_FILE=../xtal022/XDS_ASCII.HKL INPUT_FILE=../xtal023/XDS_ASCII.HKL INPUT_FILE=../xtal024/XDS_ASCII.HKL INPUT_FILE=../xtal025/XDS_ASCII.HKL INPUT_FILE=../xtal026/XDS_ASCII.HKL INPUT_FILE=../xtal027/XDS_ASCII.HKL INPUT_FILE=../xtal028/XDS_ASCII.HKL INPUT_FILE=../xtal029/XDS_ASCII.HKL INPUT_FILE=../xtal030/XDS_ASCII.HKL INPUT_FILE=../xtal031/XDS_ASCII.HKL INPUT_FILE=../xtal032/XDS_ASCII.HKL INPUT_FILE=../xtal033/XDS_ASCII.HKL INPUT_FILE=../xtal034/XDS_ASCII.HKL INPUT_FILE=../xtal035/XDS_ASCII.HKL INPUT_FILE=../xtal036/XDS_ASCII.HKL INPUT_FILE=../xtal037/XDS_ASCII.HKL INPUT_FILE=../xtal038/XDS_ASCII.HKL INPUT_FILE=../xtal039/XDS_ASCII.HKL INPUT_FILE=../xtal040/XDS_ASCII.HKL INPUT_FILE=../xtal041/XDS_ASCII.HKL INPUT_FILE=../xtal042/XDS_ASCII.HKL INPUT_FILE=../xtal043/XDS_ASCII.HKL INPUT_FILE=../xtal044/XDS_ASCII.HKL INPUT_FILE=../xtal045/XDS_ASCII.HKL INPUT_FILE=../xtal046/XDS_ASCII.HKL INPUT_FILE=../xtal047/XDS_ASCII.HKL INPUT_FILE=../xtal048/XDS_ASCII.HKL INPUT_FILE=../xtal049/XDS_ASCII.HKL INPUT_FILE=../xtal050/XDS_ASCII.HKL INPUT_FILE=../xtal051/XDS_ASCII.HKL INPUT_FILE=../xtal052/XDS_ASCII.HKL INPUT_FILE=../xtal053/XDS_ASCII.HKL INPUT_FILE=../xtal054/XDS_ASCII.HKL INPUT_FILE=../xtal055/XDS_ASCII.HKL INPUT_FILE=../xtal056/XDS_ASCII.HKL INPUT_FILE=../xtal057/XDS_ASCII.HKL INPUT_FILE=../xtal058/XDS_ASCII.HKL INPUT_FILE=../xtal059/XDS_ASCII.HKL INPUT_FILE=../xtal060/XDS_ASCII.HKL INPUT_FILE=../xtal061/XDS_ASCII.HKL INPUT_FILE=../xtal062/XDS_ASCII.HKL INPUT_FILE=../xtal063/XDS_ASCII.HKL INPUT_FILE=../xtal064/XDS_ASCII.HKL INPUT_FILE=../xtal065/XDS_ASCII.HKL INPUT_FILE=../xtal066/XDS_ASCII.HKL INPUT_FILE=../xtal067/XDS_ASCII.HKL INPUT_FILE=../xtal068/XDS_ASCII.HKL INPUT_FILE=../xtal069/XDS_ASCII.HKL INPUT_FILE=../xtal070/XDS_ASCII.HKL INPUT_FILE=../xtal071/XDS_ASCII.HKL INPUT_FILE=../xtal072/XDS_ASCII.HKL INPUT_FILE=../xtal073/XDS_ASCII.HKL INPUT_FILE=../xtal074/XDS_ASCII.HKL INPUT_FILE=../xtal075/XDS_ASCII.HKL INPUT_FILE=../xtal076/XDS_ASCII.HKL INPUT_FILE=../xtal077/XDS_ASCII.HKL INPUT_FILE=../xtal078/XDS_ASCII.HKL INPUT_FILE=../xtal079/XDS_ASCII.HKL INPUT_FILE=../xtal080/XDS_ASCII.HKL INPUT_FILE=../xtal081/XDS_ASCII.HKL INPUT_FILE=../xtal082/XDS_ASCII.HKL INPUT_FILE=../xtal083/XDS_ASCII.HKL INPUT_FILE=../xtal084/XDS_ASCII.HKL INPUT_FILE=../xtal085/XDS_ASCII.HKL INPUT_FILE=../xtal086/XDS_ASCII.HKL INPUT_FILE=../xtal087/XDS_ASCII.HKL INPUT_FILE=../xtal088/XDS_ASCII.HKL INPUT_FILE=../xtal089/XDS_ASCII.HKL INPUT_FILE=../xtal090/XDS_ASCII.HKL INPUT_FILE=../xtal091/XDS_ASCII.HKL INPUT_FILE=../xtal092/XDS_ASCII.HKL INPUT_FILE=../xtal093/XDS_ASCII.HKL INPUT_FILE=../xtal094/XDS_ASCII.HKL INPUT_FILE=../xtal095/XDS_ASCII.HKL INPUT_FILE=../xtal096/XDS_ASCII.HKL INPUT_FILE=../xtal097/XDS_ASCII.HKL INPUT_FILE=../xtal098/XDS_ASCII.HKL INPUT_FILE=../xtal099/XDS_ASCII.HKL INPUT_FILE=../xtal100/XDS_ASCII.HKL
xscale writes XSCALE.LP which has the 5050 correlation coefficients of every dataset with every other dataset! The order of listing of the correlation coefficients is such that it turns out that is was a good choice to have xtal100 as the REFERENCE_DATA_SET, because we find this list:
CORRELATIONS BETWEEN INPUT DATA SETS AFTER CORRECTIONS DATA SETS NUMBER OF COMMON CORRELATION RATIO OF COMMON B-FACTOR #i #j REFLECTIONS BETWEEN i,j INTENSITIES (i/j) BETWEEN i,j
with these final 99 lines:
1 100 12 0.601 0.8200 0.0085 2 100 24 0.998 0.9001 0.5637 3 100 16 0.990 0.9216 -0.2983 4 100 16 0.239 1.9141 -0.2253 5 100 31 0.996 0.9231 0.3755 6 100 22 0.997 0.9412 0.2726 7 100 11 0.976 0.8848 -0.1225 8 100 5 0.967 0.9166 0.0435 9 100 34 0.160 1.2885 0.0774 10 100 11 0.860 2.9740 -0.2614 11 100 8 0.997 0.8732 0.6032 12 100 8 0.998 1.0145 -0.4169 13 100 22 1.000 0.9313 0.1664 14 100 8 0.900 0.8040 0.2744 15 100 10 0.986 0.9510 0.1738 16 100 1 0.000 0.9685 0.0000 17 100 14 0.991 0.8700 0.3395 18 100 7 0.997 1.0546 -0.2113 19 100 23 1.000 1.0451 -0.0246 20 100 24 0.266 0.6392 0.1091 21 100 20 0.995 0.8529 0.6281 22 100 12 0.072 0.9376 -0.0406 23 100 19 0.999 0.9366 0.0670 24 100 14 0.998 1.0986 -0.7853 25 100 4 0.939 1.0483 -0.0886 26 100 26 0.993 0.9633 0.0813 27 100 30 0.990 0.9782 -0.0191 28 100 30 0.995 0.9124 -0.0781 29 100 13 0.488 2.1279 -0.2548 30 100 18 0.283 1.2442 0.0585 31 100 23 0.995 0.9249 0.4751 32 100 22 0.293 2.7799 -0.1715 33 100 7 1.000 1.0706 -0.2011 34 100 6 0.987 0.9888 -0.0007 35 100 8 0.989 0.9895 -0.1751 36 100 23 0.985 0.8494 0.3038 37 100 8 0.966 0.7378 -0.0108 38 100 7 1.000 1.1335 -0.0927 39 100 11 0.982 0.9994 -0.5811 40 100 16 0.994 0.7549 0.8741 41 100 12 0.986 0.9478 -0.4168 42 100 11 0.994 0.8285 0.7668 43 100 9 0.997 0.9595 -0.2219 44 100 15 1.000 0.8666 0.2884 45 100 13 0.517 1.6433 0.0034 46 100 13 0.296 1.4431 -0.0938 47 100 18 0.857 0.9734 0.3337 48 100 13 0.999 0.9627 0.2611 49 100 22 0.991 0.8798 0.2976 50 100 14 0.999 1.1206 -1.0748 51 100 10 0.999 0.9296 0.5194 52 100 8 0.899 1.3901 0.0190 53 100 24 0.998 1.0383 -0.3979 54 100 7 0.998 1.1332 -0.5519 55 100 8 0.993 0.9258 -0.0688 56 100 19 0.992 0.9138 0.0326 57 100 5 0.994 0.9209 -0.2679 58 100 22 0.996 0.8591 0.6813 59 100 7 0.650 1.5471 -0.0597 60 100 21 0.995 0.9013 0.0722 61 100 16 0.998 0.8689 0.4326 62 100 1 0.002 0.7717 0.0000 63 100 6 0.995 0.9921 0.0243 64 100 14 0.998 0.9398 -0.5243 65 100 12 0.515 1.7489 -0.0858 66 100 17 0.999 0.9457 0.0390 67 100 9 0.840 0.7706 0.5165 68 100 6 0.969 0.9477 0.0164 69 100 12 0.999 0.9503 -0.1039 70 100 10 0.949 0.8026 -0.1336 71 100 4 0.689 2.0681 0.0039 72 100 29 0.999 1.1291 -0.6696 73 100 5 -0.316 0.4326 0.0269 74 100 13 -0.233 1.4081 -0.0231 75 100 21 0.991 0.9722 -0.0179 76 100 27 0.996 0.9971 -0.7051 77 100 26 0.090 0.9911 0.0042 78 100 33 0.999 1.0320 -0.1129 79 100 19 0.990 0.9761 -0.1856 80 100 9 -0.405 0.6967 0.0026 81 100 37 1.000 0.9449 -0.3532 82 100 39 0.998 0.9688 -0.3311 83 100 16 0.996 0.9339 0.3853 84 100 4 0.999 0.8844 0.1728 85 100 0 0.000 1.0000 0.0000 86 100 4 1.000 1.0431 -0.8447 87 100 20 0.998 0.9432 0.0283 88 100 16 0.999 0.9415 0.2914 89 100 39 0.995 0.9713 -0.2225 90 100 15 0.992 1.0039 0.0773 91 100 7 0.997 1.0149 -0.4369 92 100 15 0.713 0.9845 -0.0447 93 100 21 0.249 0.8322 -0.0360 94 100 34 0.997 0.9991 -0.1059 95 100 6 0.582 0.6511 0.1327 96 100 8 0.988 0.8068 0.5740 97 100 16 0.989 0.9331 0.4112 98 100 13 0.974 0.9556 0.0624 99 100 15 0.400 0.5817 -0.0325
We note that there are many datasets with high correlation coefficients. We use some of those to generate the REFERENCE_DATA_SET for the second round - XSCALE.INP is now
OUTPUT_FILE=../reference.ahkl INPUT_FILE=../xtal002/XDS_ASCII.HKL INPUT_FILE=../xtal003/XDS_ASCII.HKL INPUT_FILE=../xtal005/XDS_ASCII.HKL INPUT_FILE=../xtal006/XDS_ASCII.HKL INPUT_FILE=../xtal007/XDS_ASCII.HKL INPUT_FILE=../xtal008/XDS_ASCII.HKL INPUT_FILE=../xtal011/XDS_ASCII.HKL INPUT_FILE=../xtal012/XDS_ASCII.HKL INPUT_FILE=../xtal013/XDS_ASCII.HKL INPUT_FILE=../xtal015/XDS_ASCII.HKL INPUT_FILE=../xtal017/XDS_ASCII.HKL INPUT_FILE=../xtal018/XDS_ASCII.HKL INPUT_FILE=../xtal019/XDS_ASCII.HKL INPUT_FILE=../xtal100/XDS_ASCII.HKL
we could have included more datasets but it's pretty clear that these 14 already provide a completeness of 34.5% :
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 111 92 304 30.3% 3.1% 4.2% 34 17.02 4.1% 3.7% 0% 0.000 0
5.69 198 161 515 31.3% 3.5% 3.4% 70 16.78 4.8% 3.6% 0% 0.000 0
4.65 289 230 639 36.0% 3.2% 3.5% 109 16.77 4.4% 3.8% 0% 0.000 0
4.03 354 267 753 35.5% 3.4% 3.6% 151 18.70 4.5% 3.1% -40% 1.012 2
3.60 367 287 840 34.2% 2.4% 3.6% 147 17.35 3.2% 3.1% 0% 0.000 0
3.29 408 326 919 35.5% 3.7% 3.6% 158 16.91 5.1% 4.0% 0% 0.000 0
3.04 422 324 987 32.8% 3.8% 3.9% 180 14.95 5.1% 4.0% 0% 0.000 0
2.85 498 387 1066 36.3% 5.2% 4.6% 212 12.72 7.1% 7.3% 0% 0.000 0
2.68 523 402 1124 35.8% 5.5% 5.4% 219 11.28 7.4% 7.2% 0% 0.000 0
2.55 512 399 1174 34.0% 5.8% 6.0% 210 9.98 7.9% 7.6% 0% 0.000 0
2.43 558 426 1263 33.7% 8.7% 8.6% 237 8.37 11.7% 12.6% -100% 0.829 2
2.32 589 446 1287 34.7% 8.1% 9.0% 261 8.05 11.0% 14.0% 61% 0.690 3
2.23 621 470 1350 34.8% 9.6% 10.4% 276 7.52 12.9% 16.8% 0% 0.000 0
2.15 653 487 1380 35.3% 8.0% 8.8% 298 7.70 10.8% 13.5% -2% 0.783 6
2.08 624 493 1459 33.8% 11.6% 11.6% 247 6.57 16.0% 16.0% 0% 0.000 0
2.01 660 510 1494 34.1% 11.3% 11.5% 271 6.16 15.0% 16.7% -100% 0.382 2
1.95 697 535 1546 34.6% 13.1% 13.8% 295 5.34 17.7% 22.9% 0% 0.000 0
1.90 765 576 1571 36.7% 15.9% 16.3% 351 5.12 21.7% 23.9% 0% 0.000 0
1.85 751 563 1635 34.4% 21.7% 22.0% 339 3.80 29.3% 35.2% 0% 0.000 0
1.80 697 531 1660 32.0% 24.5% 25.5% 298 3.51 33.1% 40.5% -11% 0.784 2
total 10297 7912 22966 34.5% 5.6% 5.9% 4363 9.17 7.6% 11.5% -9% 0.741 24
second round of bootstrap
Now we are ready to run our script "bootstrap.rc" a second time. Actually it would be enough to run the CORRECT step but since it only takes 2 minutes we don't bother to change the script. After this, we run xscale a third time, using the same XSCALE.INP (with all its 100 INPUT_FILE= lines) as the first time. The result is
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 794 270 304 88.8% 4.4% 4.2% 729 23.94 5.1% 3.0% 76% 1.884 48
5.69 1495 478 515 92.8% 4.6% 4.5% 1404 23.48 5.4% 3.3% 73% 1.633 80
4.65 1936 598 639 93.6% 5.4% 5.3% 1827 24.31 6.3% 3.7% 66% 1.541 133
4.03 2381 714 752 94.9% 4.5% 4.8% 2266 24.56 5.3% 3.2% 47% 1.157 151
3.60 2536 786 841 93.5% 5.5% 5.8% 2409 23.59 6.6% 3.9% 46% 1.164 173
3.29 2832 875 918 95.3% 5.5% 5.7% 2693 23.10 6.5% 3.8% 31% 1.013 189
3.04 3132 916 987 92.8% 5.7% 5.9% 3014 21.78 6.7% 3.8% 19% 0.917 228
2.85 3383 1014 1067 95.0% 7.1% 7.1% 3234 18.61 8.3% 5.7% 26% 0.963 233
2.68 3688 1079 1126 95.8% 8.3% 8.2% 3545 16.88 9.7% 6.9% 16% 0.911 270
2.55 3709 1109 1171 94.7% 9.6% 9.8% 3530 14.93 11.3% 8.5% 15% 0.855 252
2.43 4037 1194 1266 94.3% 10.8% 11.5% 3855 12.86 12.7% 11.1% 9% 0.805 287
2.32 4160 1217 1281 95.0% 11.7% 12.4% 3979 12.14 13.6% 10.1% 13% 0.886 312
2.23 4349 1286 1354 95.0% 12.1% 12.9% 4181 11.73 14.3% 13.5% 8% 0.738 317
2.15 4599 1324 1378 96.1% 13.6% 14.3% 4416 11.26 15.9% 12.9% 5% 0.841 341
2.08 4726 1379 1459 94.5% 15.5% 16.6% 4548 9.98 18.1% 14.6% -3% 0.784 352
2.01 4729 1419 1500 94.6% 15.6% 16.5% 4521 9.46 18.3% 16.4% 6% 0.818 338
1.95 4980 1480 1544 95.9% 20.3% 20.3% 4782 8.20 23.9% 21.1% -2% 0.778 353
1.90 5217 1511 1575 95.9% 22.7% 23.7% 5016 7.51 26.5% 23.6% -4% 0.740 391
1.85 5232 1555 1626 95.6% 29.8% 31.0% 5015 5.91 34.9% 28.6% 5% 0.813 359
1.80 5024 1511 1669 90.5% 33.5% 34.6% 4790 5.25 39.4% 36.9% -1% 0.767 347
total 72939 21715 22972 94.5% 8.2% 8.5% 69754 13.36 9.7% 10.3% 16% 0.891 5154
so the data are practically complete, and actually quite good. The anomalous signal suggests that it may be possible to solve the structure from its anomalous signal.
We can find out the correct spacegroup (19 !) with "pointless xdsin temp.ahkl", and adjust our script accordingly.
Now we do another round, since the completeness is so good. We can then identify those few datasets which are still not indexed in the right setting, and fix those manually. It was only xtal085 which had a problem - it turned out that the indexing had not found the correct lattice, which was fixed with STRONG_PIXEL=6.
The final XSCALE.LP is then:
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 804 276 316 87.3% 4.4% 4.2% 733 23.80 5.1% 3.1% 75% 1.899 49
5.69 1509 481 520 92.5% 4.5% 4.4% 1416 23.61 5.2% 3.3% 75% 1.660 81
4.65 1951 601 644 93.3% 4.3% 4.4% 1842 24.49 5.1% 3.3% 68% 1.579 134
4.03 2402 715 755 94.7% 4.1% 4.4% 2289 24.75 4.8% 3.2% 44% 1.174 153
3.60 2555 788 843 93.5% 4.0% 4.5% 2427 23.81 4.7% 3.2% 48% 1.169 179
3.29 2862 877 921 95.2% 4.2% 4.7% 2724 23.35 5.0% 3.2% 31% 1.050 198
3.04 3146 916 989 92.6% 5.0% 5.1% 3030 22.00 5.8% 4.0% 15% 0.897 231
2.85 3399 1016 1070 95.0% 5.9% 6.1% 3251 18.75 7.0% 5.4% 28% 0.992 235
2.68 3717 1081 1128 95.8% 7.2% 7.2% 3579 17.01 8.4% 7.1% 13% 0.883 274
2.55 3724 1110 1174 94.5% 8.3% 8.6% 3543 15.03 9.7% 8.0% 15% 0.836 255
2.43 4058 1196 1266 94.5% 9.9% 10.6% 3877 12.96 11.5% 10.3% 8% 0.811 291
2.32 4190 1220 1283 95.1% 11.1% 11.8% 4013 12.21 12.9% 10.8% 11% 0.889 328
2.23 4371 1288 1357 94.9% 11.5% 12.4% 4207 11.79 13.6% 12.6% 4% 0.757 318
2.15 4626 1324 1378 96.1% 13.2% 13.9% 4444 11.33 15.4% 12.4% 8% 0.835 349
2.08 4756 1383 1461 94.7% 15.2% 16.2% 4577 10.02 17.8% 14.2% -4% 0.771 356
2.01 4755 1423 1503 94.7% 15.4% 16.1% 4543 9.51 18.1% 15.2% 5% 0.817 342
1.95 4995 1480 1544 95.9% 20.1% 19.9% 4794 8.24 23.6% 20.2% -5% 0.787 359
1.90 5242 1512 1577 95.9% 22.3% 23.2% 5034 7.55 26.1% 22.2% -1% 0.772 400
1.85 5261 1552 1626 95.4% 29.6% 30.6% 5054 5.95 34.6% 28.3% 6% 0.828 365
1.80 5066 1514 1672 90.6% 33.4% 34.4% 4829 5.25 39.2% 35.7% -1% 0.789 356
total 73389 21753 23027 94.5% 7.4% 7.7% 70206 13.45 8.6% 9.8% 15% 0.898 5253
When inspecting the list of R-factors of each of the datasets it becomes clear that some of them are really good, but others are mediocre.
Optimizing the result
One method to improve XDS' knowledge of geometry would be to use all 15 frames for indexing, but still only to integrate frame 1. This is easily accomplished by changing in the script:
JOB=XYCORR INIT COLSPOT IDXREF DEFPIX DATA_RANGE=1 15 SPOT_RANGE=1 15
and to use, instead of "xds >& xds.log &" the line "../../run_xds.rc &" with the following run_xds.rc :
#!/bin/csh -f xds egrep -v 'DATA_RANGE|JOB' XDS.INP >x echo JOB=INTEGRATE CORRECT >XDS.INP echo DATA_RANGE=1 1 >> XDS.INP cat x >> XDS.INP xds
Furthermore it seems good to change "sleep 1" to "sleep 5" because now each COLSPOT has to look at 15 frames, not one. Thus, this takes a little bit longer. Indeed the result is a bit better:
WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 798 274 304 90.1% 4.4% 4.2% 726 23.88 5.2% 3.1% 71% 1.932 49
5.69 1514 480 515 93.2% 4.5% 4.5% 1421 23.66 5.3% 3.4% 76% 1.670 83
4.65 1951 599 639 93.7% 4.3% 4.4% 1845 24.57 5.0% 3.3% 67% 1.561 139
4.03 2399 713 753 94.7% 4.1% 4.5% 2289 24.76 4.8% 3.1% 44% 1.176 154
3.60 2546 786 840 93.6% 3.9% 4.5% 2417 23.78 4.6% 3.1% 46% 1.127 175
3.29 2864 876 919 95.3% 4.2% 4.7% 2729 23.35 4.9% 3.2% 38% 1.018 199
3.04 3154 918 987 93.0% 5.0% 5.2% 3037 21.98 5.8% 3.9% 18% 0.922 231
2.85 3387 1015 1066 95.2% 5.9% 6.1% 3235 18.74 7.0% 5.2% 26% 0.992 235
2.68 3724 1082 1126 96.1% 7.2% 7.2% 3583 17.03 8.4% 6.7% 15% 0.890 278
2.55 3720 1111 1172 94.8% 8.3% 8.6% 3536 15.02 9.7% 8.1% 14% 0.857 255
2.43 4079 1198 1267 94.6% 9.8% 10.6% 3898 12.96 11.5% 10.3% 9% 0.781 290
2.32 4199 1221 1283 95.2% 11.1% 11.7% 4024 12.21 12.9% 10.8% 12% 0.911 331
2.23 4365 1282 1350 95.0% 11.4% 12.2% 4205 11.87 13.4% 12.6% 3% 0.729 319
2.15 4651 1332 1386 96.1% 13.3% 13.9% 4468 11.30 15.5% 12.5% 5% 0.821 354
2.08 4745 1380 1455 94.8% 15.0% 16.0% 4569 10.04 17.6% 14.0% -1% 0.760 358
2.01 4744 1418 1496 94.8% 15.4% 16.0% 4531 9.50 18.1% 16.3% 5% 0.820 343
1.95 5019 1487 1550 95.9% 19.6% 19.7% 4813 8.27 23.0% 19.7% -1% 0.765 359
1.90 5210 1504 1571 95.7% 21.9% 22.9% 5007 7.53 25.6% 22.8% -6% 0.740 399
1.85 5272 1561 1633 95.6% 29.1% 30.1% 5054 5.98 34.1% 28.8% 4% 0.801 366
1.80 5054 1505 1659 90.7% 33.2% 34.1% 4822 5.25 38.9% 35.2% -1% 0.790 354
total 73395 21742 22971 94.6% 7.3% 7.7% 70209 13.46 8.6% 9.8% 16% 0.890 5271
but there does not appear a "magic bullet" that would produce much better data than with the quick bootstrap approach.
Trying to solve the structure
First, we repeat xscale after inserting FRIEDEL'S_LAW=FALSE into XSCALE.INP . This gives us
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 804 382 476 80.3% 3.1% 3.4% 665 24.13 3.9% 2.7% 81% 2.507 50
5.69 1527 723 882 82.0% 3.4% 3.6% 1251 22.48 4.2% 3.1% 85% 2.223 87
4.65 1956 938 1136 82.6% 3.4% 3.6% 1602 22.73 4.3% 3.0% 72% 1.821 141
4.03 2400 1136 1357 83.7% 3.5% 3.6% 1943 22.62 4.4% 3.2% 46% 1.347 154
3.60 2549 1261 1533 82.3% 3.4% 3.7% 2053 21.53 4.3% 3.3% 51% 1.322 176
3.29 2867 1393 1694 82.2% 3.7% 3.9% 2347 21.22 4.7% 3.5% 35% 1.159 199
3.04 3154 1507 1830 82.3% 4.5% 4.3% 2607 19.33 5.7% 4.5% 17% 1.016 231
2.85 3389 1649 1979 83.3% 5.3% 5.2% 2761 16.37 6.7% 6.0% 27% 1.054 235
2.68 3724 1757 2104 83.5% 6.5% 6.1% 3088 14.63 8.1% 7.8% 15% 0.962 278
2.55 3720 1813 2197 82.5% 7.3% 7.6% 2999 12.84 9.2% 9.1% 16% 0.896 255
2.43 4079 1933 2384 81.1% 9.0% 9.5% 3352 11.01 11.3% 12.5% 9% 0.840 290
2.32 4199 2006 2420 82.9% 10.0% 10.5% 3474 10.17 12.7% 13.8% 14% 0.939 331
2.23 4363 2099 2551 82.3% 10.6% 11.0% 3595 9.91 13.4% 14.5% 5% 0.790 319
2.15 4651 2203 2634 83.6% 12.2% 12.5% 3827 9.29 15.3% 15.7% 7% 0.856 354
2.08 4745 2248 2758 81.5% 14.2% 14.7% 3945 8.32 18.0% 18.7% -2% 0.822 358
2.01 4744 2287 2843 80.4% 14.3% 14.6% 3896 7.92 18.1% 19.2% 7% 0.868 343
1.95 5019 2429 2945 82.5% 18.5% 18.3% 4079 6.76 23.3% 24.6% 0% 0.789 359
1.90 5210 2484 3000 82.8% 20.4% 21.0% 4282 6.06 25.6% 27.9% -4% 0.757 399
1.85 5272 2569 3119 82.4% 27.8% 28.0% 4272 4.77 35.0% 36.5% 4% 0.803 366
1.80 5054 2451 3171 77.3% 30.9% 31.1% 4092 4.20 39.0% 43.1% -3% 0.788 354
total 73426 35268 43013 82.0% 6.5% 6.7% 60130 11.57 8.2% 11.7% 20% 0.963 5279
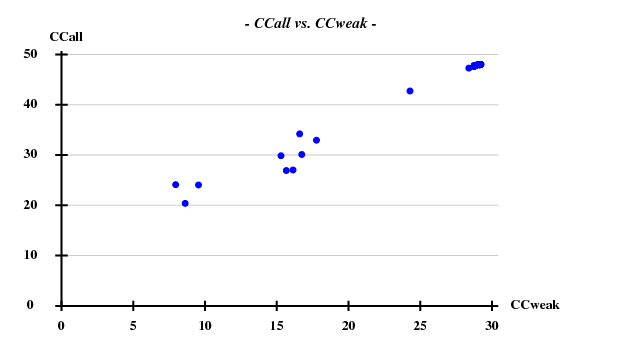
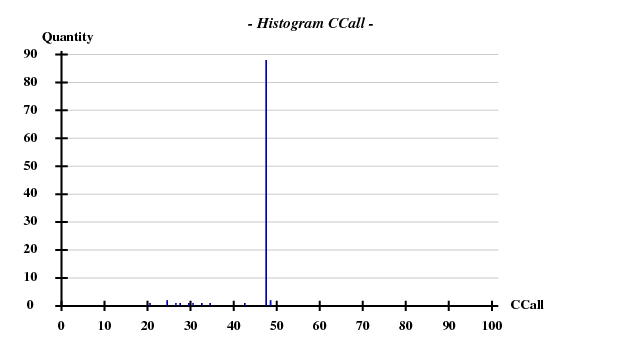
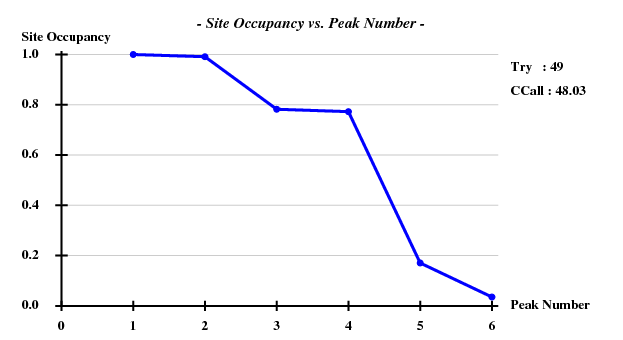
One hint towards the contents of the "crystal" is that the information about the simulated data contained the strings "1g1c". This structure (spacegroup 19, cell axes 38.3, 78.6, 79.6) is available from the PDB; it contains 2 chains of 99 residues, and a chain has 2 Cys and 2 Met. Thus we assume that the simulated data may represent SeMet-SAD. Using hkl2map, we can easily find four sites with good CCall/CCweak:
I also tried the poly-Ala tracing feature of shelxe:
shelxe.beta -m40 -a -q -h -s0.54 -b -i -e -n 1g1c 1g1c_fa
but it traces only about 62 residues. The density looks somewhat reasonable, though.
The files xds-simulated-1g1c-I.mtz and xds-simulated-1g1c-F.mtz are available.
I refined against 1g1c.pdb:
phenix.refine xds-simulated-1g1c-F.mtz 1g1c.pdb refinement.input.xray_data.r_free_flags.generate=True
The result was
Start R-work = 0.3453, R-free = 0.3501 Final R-work = 0.2170, R-free = 0.2596
which appears reasonable.
Notes
Towards better completeness: using the first two frames instead of only the first
We might want better (anomalous) completeness than what is given by only the very first frame of each dataset. To this end, we change in the XDS.INP part of our script :
DATA_RANGE=1 2
then run the script which reduces the 100 datasets. When this has finished, we insert in XSCALE.INP
NBATCH=2
after each INPUT_FILE line (this can be easily done using
awk '{print $0;print "NBATCH=2"}' XSCALE.INP > x ). The reason for this is that by default, XSCALE establishes scalefactors every 5 degrees, but here we want scalefactors for every frame, because the radiation damage is so strong. This gives:
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 1922 467 476 98.1% 4.2% 6.6% 1888 20.04 4.8% 2.8% 84% 1.887 142
5.69 3494 864 882 98.0% 4.5% 6.8% 3429 18.67 5.2% 3.1% 83% 1.635 297
4.65 4480 1111 1136 97.8% 5.3% 6.7% 4395 18.89 6.1% 3.5% 66% 1.347 406
4.03 5197 1325 1357 97.6% 6.2% 6.8% 5101 18.37 7.1% 4.3% 43% 1.156 499
3.60 5916 1500 1533 97.8% 6.9% 7.1% 5804 17.83 8.0% 4.7% 36% 1.083 572
3.29 6601 1657 1694 97.8% 7.6% 7.3% 6476 17.26 8.7% 4.9% 24% 1.029 634
3.04 7081 1789 1830 97.8% 9.1% 8.0% 6949 15.50 10.4% 6.4% 17% 1.011 693
2.85 7684 1946 1979 98.3% 10.9% 9.9% 7530 12.95 12.5% 8.1% 16% 0.950 751
2.68 8101 2062 2100 98.2% 13.1% 12.1% 7935 11.18 15.0% 10.5% 10% 0.888 795
2.55 8355 2156 2201 98.0% 15.2% 14.9% 8182 9.69 17.5% 12.3% 6% 0.867 837
2.43 9195 2327 2376 97.9% 18.2% 18.6% 9003 8.20 20.8% 15.4% 6% 0.837 904
2.32 9495 2377 2428 97.9% 21.3% 21.9% 9304 7.42 24.4% 18.4% 6% 0.800 934
2.23 9939 2499 2551 98.0% 23.0% 23.3% 9753 7.13 26.4% 19.0% 4% 0.818 987
2.15 10219 2577 2622 98.3% 25.4% 25.9% 9992 6.63 29.1% 20.6% 1% 0.797 998
2.08 10712 2704 2766 97.8% 29.4% 30.8% 10508 5.80 33.8% 25.1% 4% 0.793 1071
2.01 10900 2778 2839 97.9% 30.8% 31.2% 10649 5.50 35.3% 26.2% 4% 0.828 1060
1.95 11361 2878 2937 98.0% 36.7% 38.2% 11134 4.71 42.1% 31.5% 1% 0.768 1136
1.90 11641 2943 3000 98.1% 42.7% 45.1% 11405 4.12 49.1% 38.7% -1% 0.775 1165
1.85 12028 3069 3123 98.3% 54.0% 60.4% 11760 3.19 62.1% 47.5% 5% 0.735 1196
1.80 11506 3003 3173 94.6% 62.1% 70.6% 11229 2.72 71.6% 60.6% -2% 0.709 1148
total 165827 42032 43003 97.7% 12.8% 13.3% 162426 8.79 14.7% 15.7% 15% 0.881 16225
showing that the anomalous completeness, and even the quality of the anomalous signal, can indeed be increased. I doubt, however, that going to three or more frames would improve things even more.
The MTZ files are at [2] and [3], respectively. They were of course obtained with XDSCONV.INP:
INPUT_FILE=temp.ahkl OUTPUT_FILE=temp.hkl CCP4_I
for the intensities, and
INPUT_FILE=temp.ahkl OUTPUT_FILE=temp.hkl CCP4
for the amplitudes. In both cases, after xdsconv we have to run
f2mtz HKLOUT temp.mtz<F2MTZ.INP cad HKLIN1 temp.mtz HKLOUT output_file_name.mtz<<EOF LABIN FILE 1 ALL END EOF
Using the default (see above) phenix.refine job, I obtain against the MTZ file with amplitudes:
Start R-work = 0.3434, R-free = 0.3540 Final R-work = 0.2209, R-free = 0.2479
and against the MTZ file with intensities
Start R-work = 0.3492, R-free = 0.3606 Final R-work = 0.2244, R-free = 0.2504
so: better R-free is obtained from better data.
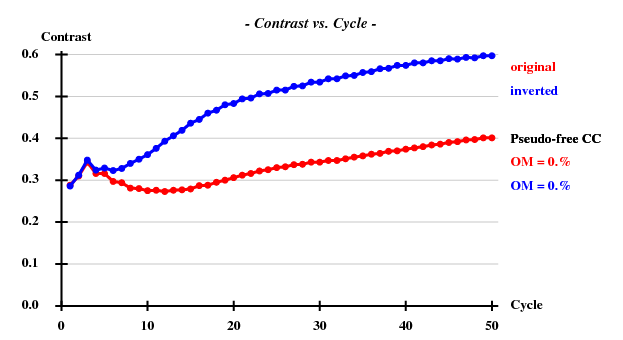
The statistics from SHELXD and SHELXE don't look better - they were already quite good with a single frame per dataset. The statistics printed by SHELXE (for the correct hand) are:
... <wt> = 0.300, Contrast = 0.591, Connect. = 0.740 for dens.mod. cycle 50 Estimated mean FOM and mapCC as a function of resolution d inf - 3.98 - 3.13 - 2.72 - 2.47 - 2.29 - 2.15 - 2.04 - 1.95 - 1.87 - 1.81 <FOM> 0.601 0.606 0.590 0.570 0.538 0.542 0.521 0.509 0.529 0.498 <mapCC> 0.841 0.813 0.811 0.786 0.763 0.744 0.727 0.740 0.761 0.722 N 2289 2303 2334 2245 2289 2330 2299 2297 2429 2046 Estimated mean FOM = 0.551 Pseudo-free CC = 59.42 % ... Site x y z h(sig) near old near new 1 0.7375 0.6996 0.1537 20.4 1/0.06 2/15.05 6/21.38 3/21.54 5/22.03 2 0.7676 0.7231 0.3419 18.8 3/0.13 5/12.15 1/15.05 3/21.34 4/22.43 3 0.5967 0.4904 -0.0067 17.2 4/0.10 4/4.90 6/4.94 2/21.34 1/21.54 4 0.5269 0.5194 -0.0498 17.1 2/0.05 3/4.90 6/7.85 2/22.43 1/22.96 5 0.4857 0.6896 0.4039 -4.8 3/12.04 2/12.15 1/22.03 3/22.55 2/22.85 6 0.5158 0.4788 0.0406 4.7 5/1.45 3/4.94 4/7.85 1/21.38 5/23.30
Why this is difficult to solve with SAD phasing
In the original publication ("Structural evidence for a possible role of reversible disulphide bridge formation in the elasticity of the muscle protein titin" Mayans, O., Wuerges, J., Canela, S., Gautel, M., Wilmanns, M. (2001) Structure 9: 331-340 ) we read:
"This crystal form contains two molecules in the asymmetric unit. They are related by a noncrystallographic two-fold axis, parallel to the crystallographic b axis, located at X = 0.25 and Z = 0.23. This arrangement results in a peak in the native Patterson map at U = 0.5, V = 0, W = 0.47 of peak height 26 σ (42% of the origin peak)."
Unfortunately, the arrangement of substructure sites has (pseudo-)translational symmetry, and may be related to a centrosymmetric arrangement. Indeed, the original structure was solved using molecular replacement.
Using the four sites as given by SHELXE (and default parameters otherwise), I obtained from the cctbx - Phase-O-Phrenia server the following
Plot of relative peak heights:
|*
|*
|*
|*
|**
|**
|***
|****
|******
|************
|********************
|*****************************
|*********************************
|***************************************
|************************************************
|************************************************************
|************************************************************
|************************************************************
|************************************************************
|************************************************************
-------------------------------------------------------------
Peak list:
Relative
height Fractional coordinates
97.8 0.01982 0.49860 -0.00250
80.2 0.17362 0.71758 0.83714
71.5 0.02405 0.53538 0.48365
63.9 -0.00511 0.07044 0.50289
62.1 0.02410 0.94827 0.48807
61.3 0.16922 0.28605 0.15985
56.3 0.12047 0.50910 0.43665
55.9 0.21871 0.26331 0.30008
55.7 0.10931 0.47245 0.53659
53.0 0.22211 0.23746 0.39503
52.9 0.03449 -0.00661 0.98264 <------ this peak is close to the origin
52.5 0.06905 0.02372 0.05632 <------ this one, too
...
so the strongest peak corresponds to the translation of molecules (0,0.5,0) but the origin peak is at 1/2 of that size, which appears significant.
Finally solving the structure
After thinking about the most likely way that James Holton used to produce the simulated data, I hypothesized that within each frame, the radiation damage is most likely constant, and that there is a jump in radiation damage from frame 1 to 2. Unfortunately for this scenario, the scaling algorithm in CORRECT and XSCALE was changed for the version of Dec-2010, such that it produces best results when the changes are smooth. Therefore, I tried the penultimate version (May-2010) of XSCALE - and indeed that gives significantly better results:
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.05 1922 467 476 98.1% 4.0% 5.8% 1888 22.37 4.5% 2.5% 84% 1.952 142
5.69 3494 864 882 98.0% 4.7% 6.0% 3429 20.85 5.4% 3.2% 77% 1.707 297
4.65 4480 1111 1136 97.8% 5.1% 5.9% 4395 21.13 5.8% 3.3% 68% 1.518 406
4.03 5197 1325 1357 97.6% 5.3% 6.0% 5101 20.57 6.1% 3.8% 48% 1.280 499
3.60 5915 1500 1533 97.8% 6.0% 6.3% 5803 19.99 6.9% 4.1% 41% 1.169 572
3.29 6601 1657 1694 97.8% 6.5% 6.5% 6476 19.42 7.5% 4.6% 27% 1.066 634
3.04 7080 1789 1830 97.8% 7.6% 7.2% 6948 17.50 8.7% 5.4% 23% 1.037 693
2.85 7682 1945 1979 98.3% 8.8% 9.0% 7528 14.75 10.1% 7.0% 15% 0.935 750
2.68 8099 2062 2100 98.2% 11.0% 11.1% 7933 12.81 12.7% 9.1% 13% 0.881 795
2.55 8351 2155 2201 97.9% 13.3% 13.7% 8178 11.16 15.4% 11.0% 12% 0.872 836
2.43 9195 2327 2376 97.9% 16.5% 17.2% 9003 9.49 19.0% 15.1% 8% 0.838 904
2.32 9495 2377 2428 97.9% 19.8% 20.3% 9304 8.62 22.7% 17.3% 4% 0.818 934
2.23 9936 2498 2551 97.9% 20.8% 21.7% 9751 8.30 23.9% 17.5% 4% 0.830 987
2.15 10217 2577 2622 98.3% 23.3% 24.0% 9990 7.74 26.7% 19.2% 4% 0.814 998
2.08 10710 2704 2766 97.8% 27.1% 28.6% 10506 6.82 31.1% 23.5% 5% 0.812 1071
2.01 10899 2777 2839 97.8% 28.1% 29.2% 10648 6.46 32.3% 25.0% 6% 0.813 1059
1.95 11361 2878 2937 98.0% 34.4% 35.5% 11134 5.55 39.5% 30.3% 3% 0.780 1136
1.90 11639 2941 3000 98.0% 40.5% 41.5% 11403 4.88 46.6% 35.9% 0% 0.787 1163
1.85 12020 3068 3123 98.2% 52.2% 55.1% 11752 3.79 60.0% 47.4% 6% 0.775 1195
1.80 11506 3003 3173 94.6% 60.8% 64.8% 11229 3.23 70.1% 58.8% 0% 0.765 1148
total 165799 42025 43003 97.7% 11.7% 12.3% 162399 10.07 13.5% 14.8% 17% 0.908 16219
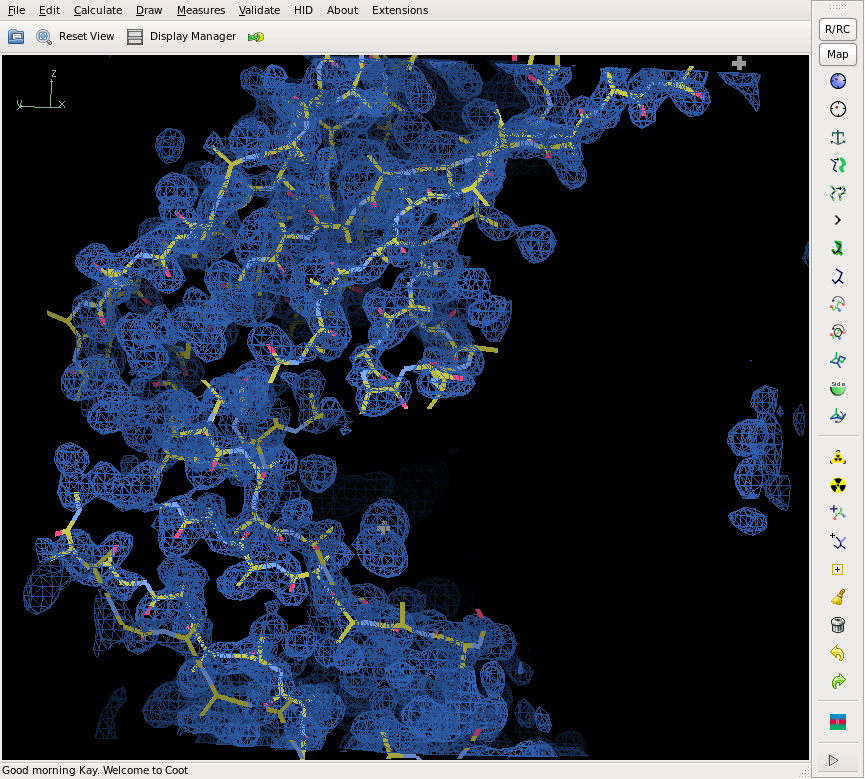
Using these data (stored in [4]), I was finally able to solve the structure (see screenshot below) - SHELXE traced 160 out of 198 residues. All files produced by SHELXE are in [5].
It is worth mentioning that James Holton confirmed that my hypothesis is true; he also says that this approach is a good approximation for a multi-pass data collection.
However, generally (i.e. for real data) the smooth scaling (which also applies to absorption correction and detector modulation) gives better results than the previous method of assigning the same scale factor to all reflections of a frame; in particular, it correctly treats those reflections near the border of two frames.
Phenix.refine against these data gives:
Start R-work = 0.3449, R-free = 0.3560 Final R-work = 0.2194, R-free = 0.2469
which is only 0.15%/0.10% better in R-work/R-free than the previous best result (see above).
This example shows that it is important to
- have the best data available if a structure is difficult to solve
- know the options (programs, algorithms)
- know as much as possible about the experiment