XDSwiki

Simulated-1g1c: Difference between revisions

Page Discussion

Simulated-1g1c (view source)

Revision as of 14:14, 24 March 2020

14,054 bytes added ,  24 March 2020
m
no edit summary
No edit summary
mNo edit summary
 
(10 intermediate revisions by 2 users not shown)
Line 530: Line 530:
but there does not appear a "magic bullet" that would produce much better data than with the quick bootstrap approach.
but there does not appear a "magic bullet" that would produce much better data than with the quick bootstrap approach.


== Solving the structure ==
== Trying to solve the structure ==


First, we repeat xscale after inserting FRIEDEL'S_LAW=FALSE into XSCALE.INP . This gives us
First, we repeat xscale after inserting FRIEDEL'S_LAW=FALSE into XSCALE.INP . This gives us
Line 562: Line 562:




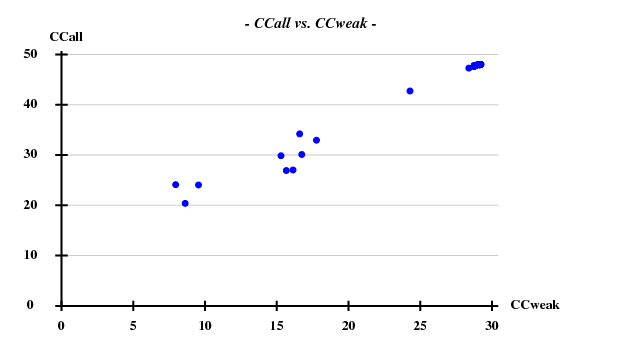
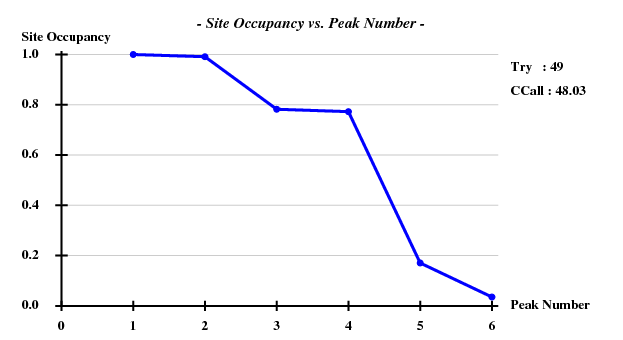
One hint towards the contents of the "crystal" is that the information about the simulated data contained the strings "1g1c". This structure is solved (in spacegroup 19, cell axes 38.3, 78.6, 79.6) and can be found in the PDB; it contains 2 chains of 99 residues, and a chain has 2 Cys and 2 Met. Thus we assume that the simulated data may represent SeMet-SAD. Using [[ccp4:hkl2map|hkl2map]], we can easily find four sites with good CCall/CCweak:
One hint towards the contents of the "crystal" is that the information about the simulated data contained the strings "1g1c". This structure (spacegroup 19, cell axes 38.3, 78.6, 79.6) is available from the PDB; it contains 2 chains of 99 residues, and a chain has 2 Cys and 2 Met. Thus we assume that the simulated data may represent SeMet-SAD. Using [[ccp4:hkl2map|hkl2map]], we can easily find four sites with good CCall/CCweak:


[[File:Simulated-1g1c-ccall-ccweak2.png]]
[[File:Simulated-1g1c-ccall-ccweak2.png]]
Line 573: Line 573:
  shelxe.beta -m40 -a -q -h -s0.54 -b -i -e -n 1g1c 1g1c_fa
  shelxe.beta -m40 -a -q -h -s0.54 -b -i -e -n 1g1c 1g1c_fa


but it traces only about 62 residues. The density looks reasonable, though.
but it traces only about 62 residues. The density looks somewhat reasonable, though.


The files [ftp::/turn5.biologie.uni-konstanz.de/pub/xds-datared/1g1c/xds-simulated-1g1c-I.mtz xds-simulated-1g1c-I.mtz] and [ftp::/turn5.biologie.uni-konstanz.de/pub/xds-datared/1g1c/xds-simulated-1g1c-F.mtz xds-simulated-1g1c-F.mtz] are available.
The files [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-I.mtz xds-simulated-1g1c-I.mtz] and [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-F.mtz xds-simulated-1g1c-F.mtz] are available.
 
I refined against 1g1c.pdb:
phenix.refine xds-simulated-1g1c-F.mtz 1g1c.pdb refinement.input.xray_data.r_free_flags.generate=True
The result was
Start R-work = 0.3453, R-free = 0.3501
Final R-work = 0.2170, R-free = 0.2596
which appears reasonable.
 
== Notes ==
 
=== Towards better completeness: using the first two frames instead of only the first ===
 
We might want better (anomalous) completeness than what is given by only the very first frame of each dataset. To this end, we change in the XDS.INP part of our script :
DATA_RANGE=1 2
then run the script which reduces the 100 datasets. When this has finished, we insert in XSCALE.INP
NBATCH=2
after each INPUT_FILE line (this can be easily done using <pre> awk '{print $0;print "NBATCH=2"}' XSCALE.INP > x </pre>). The reason for this is that by default, XSCALE establishes scalefactors every 5 degrees, but here we want scalefactors for every frame, because the radiation damage is so strong. This gives:
      NOTE:     Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION    NUMBER OF REFLECTIONS    COMPLETENESS R-FACTOR  R-FACTOR COMPARED I/SIGMA  R-meas  Rmrgd-F  Anomal  SigAno  Nano
  LIMIT    OBSERVED  UNIQUE  POSSIBLE    OF DATA  observed  expected                                      Corr
    8.05        1922    467      476      98.1%      4.2%      6.6%    1888  20.04    4.8%    2.8%    84%  1.887    142
    5.69        3494    864      882      98.0%      4.5%      6.8%    3429  18.67    5.2%    3.1%    83%  1.635    297
    4.65        4480    1111      1136      97.8%      5.3%      6.7%    4395  18.89    6.1%    3.5%    66%  1.347    406
    4.03        5197    1325      1357      97.6%      6.2%      6.8%    5101  18.37    7.1%    4.3%    43%  1.156    499
    3.60        5916    1500      1533      97.8%      6.9%      7.1%    5804  17.83    8.0%    4.7%    36%  1.083    572
    3.29        6601    1657      1694      97.8%      7.6%      7.3%    6476  17.26    8.7%    4.9%    24%  1.029    634
    3.04        7081    1789      1830      97.8%      9.1%      8.0%    6949  15.50    10.4%    6.4%    17%  1.011    693
    2.85        7684    1946      1979      98.3%      10.9%      9.9%    7530  12.95    12.5%    8.1%    16%  0.950    751
    2.68        8101    2062      2100      98.2%      13.1%    12.1%    7935  11.18    15.0%    10.5%    10%  0.888    795
    2.55        8355    2156      2201      98.0%      15.2%    14.9%    8182    9.69    17.5%    12.3%    6%  0.867    837
    2.43        9195    2327      2376      97.9%      18.2%    18.6%    9003    8.20    20.8%    15.4%    6%  0.837    904
    2.32        9495    2377      2428      97.9%      21.3%    21.9%    9304    7.42    24.4%    18.4%    6%  0.800    934
    2.23        9939    2499      2551      98.0%      23.0%    23.3%    9753    7.13    26.4%    19.0%    4%  0.818    987
    2.15      10219    2577      2622      98.3%      25.4%    25.9%    9992    6.63    29.1%    20.6%    1%  0.797    998
    2.08      10712    2704      2766      97.8%      29.4%    30.8%    10508    5.80    33.8%    25.1%    4%  0.793    1071
    2.01      10900    2778      2839      97.9%      30.8%    31.2%    10649    5.50    35.3%    26.2%    4%  0.828    1060
    1.95      11361    2878      2937      98.0%      36.7%    38.2%    11134    4.71    42.1%    31.5%    1%  0.768    1136
    1.90      11641    2943      3000      98.1%      42.7%    45.1%    11405    4.12    49.1%    38.7%    -1%  0.775    1165
    1.85      12028    3069      3123      98.3%      54.0%    60.4%    11760    3.19    62.1%    47.5%    5%  0.735    1196
    1.80      11506    3003      3173      94.6%      62.1%    70.6%    11229    2.72    71.6%    60.6%    -2%  0.709    1148
    total      165827  42032    43003      97.7%      12.8%    13.3%  162426    8.79    14.7%    15.7%    15%  0.881  16225
 
showing that the anomalous completeness, and even the quality of the anomalous signal, can indeed be increased. I doubt, however, that going to three or more frames would improve things even more.
 
The MTZ files are at [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-F-2frames.mtz] and [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-I-2frames.mtz], respectively. They were of course obtained with XDSCONV.INP:
INPUT_FILE=temp.ahkl
OUTPUT_FILE=temp.hkl CCP4_I
for the intensities, and
INPUT_FILE=temp.ahkl
OUTPUT_FILE=temp.hkl CCP4
for the amplitudes. In both cases, after xdsconv we have to run
<pre>
f2mtz HKLOUT temp.mtz<F2MTZ.INP
cad HKLIN1 temp.mtz HKLOUT output_file_name.mtz<<EOF
LABIN FILE 1 ALL
END
EOF
</pre>
 
Using the default (see above) phenix.refine job, I obtain against the [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-F-2frames.mtz MTZ file with amplitudes]:
Start R-work = 0.3434, R-free = 0.3540
Final R-work = 0.2209, R-free = 0.2479
and against the [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xds-simulated-1g1c-I-2frames.mtz MTZ file with intensities]
Start R-work = 0.3492, R-free = 0.3606
Final R-work = 0.2244, R-free = 0.2504
 
so: '''better R-free is obtained from better data.'''
 
The statistics from SHELXD and SHELXE don't look better - they were already quite good with a single frame per dataset. The statistics printed by SHELXE (for the correct hand) are:
...
<wt> = 0.300, Contrast = 0.591, Connect. = 0.740 for dens.mod. cycle 50
Estimated mean FOM and mapCC as a function of resolution
d    inf - 3.98 - 3.13 - 2.72 - 2.47 - 2.29 - 2.15 - 2.04 - 1.95 - 1.87 - 1.81
<FOM>  0.601  0.606  0.590  0.570  0.538  0.542  0.521  0.509  0.529  0.498
<mapCC> 0.841  0.813  0.811  0.786  0.763  0.744  0.727  0.740  0.761  0.722
N        2289  2303  2334  2245  2289  2330  2299  2297  2429  2046
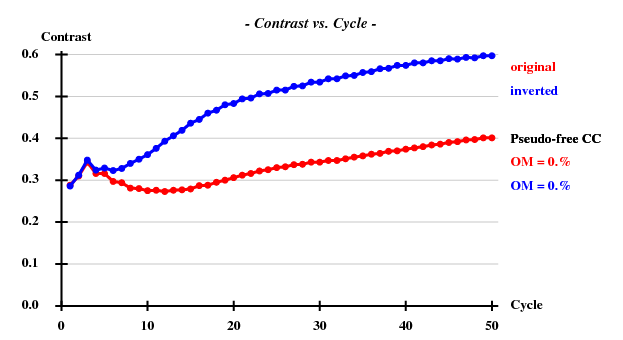
Estimated mean FOM = 0.551  Pseudo-free CC = 59.42 %
...
Site    x      y      z  h(sig) near old  near new
  1  0.7375  0.6996  0.1537  20.4  1/0.06  2/15.05 6/21.38 3/21.54 5/22.03
  2  0.7676  0.7231  0.3419  18.8  3/0.13  5/12.15 1/15.05 3/21.34 4/22.43
  3  0.5967  0.4904 -0.0067  17.2  4/0.10  4/4.90 6/4.94 2/21.34 1/21.54
  4  0.5269  0.5194 -0.0498  17.1  2/0.05  3/4.90 6/7.85 2/22.43 1/22.96
  5  0.4857  0.6896  0.4039  -4.8  3/12.04  2/12.15 1/22.03 3/22.55 2/22.85
  6  0.5158  0.4788  0.0406  4.7  5/1.45  3/4.94 4/7.85 1/21.38 5/23.30
 
=== Why this is difficult to solve with SAD phasing ===
 
In the original publication ("Structural evidence for a possible role of reversible disulphide bridge formation in the elasticity of the muscle protein titin" Mayans, O., Wuerges, J., Canela, S., Gautel, M., Wilmanns, M. (2001) Structure 9: 331-340 ) we read:
 
"This crystal form contains two molecules in the asymmetric unit. They are related by a noncrystallographic two-fold axis, parallel to the crystallographic b axis, located at X = 0.25 and Z = 0.23. This arrangement results in a peak in the native Patterson map at U = 0.5, V = 0, W = 0.47 of peak height 26 σ (42% of the origin peak)."
 
Unfortunately, the arrangement of substructure sites has (pseudo-)translational symmetry, and may be related to a centrosymmetric arrangement. Indeed, the original structure was solved using molecular replacement.
 
Using the four sites as given by SHELXE (and default parameters otherwise), I obtained from the [http://cci.lbl.gov/cctbx/phase_o_phrenia.html cctbx - Phase-O-Phrenia server] the following
Plot of relative peak heights:
    |*
    |*
    |*
    |*
    |**
    |**
    |***
    |****
    |******
    |************
    |********************
    |*****************************
    |*********************************
    |***************************************
    |************************************************
    |************************************************************
    |************************************************************
    |************************************************************
    |************************************************************
    |************************************************************
    -------------------------------------------------------------
Peak list:
  Relative
  height  Fractional coordinates
    97.8  0.01982  0.49860 -0.00250
    80.2  0.17362  0.71758  0.83714
    71.5  0.02405  0.53538  0.48365
    63.9  -0.00511  0.07044  0.50289
    62.1  0.02410  0.94827  0.48807
    61.3  0.16922  0.28605  0.15985
    56.3  0.12047  0.50910  0.43665
    55.9  0.21871  0.26331  0.30008
    55.7  0.10931  0.47245  0.53659
    53.0  0.22211  0.23746  0.39503
    52.9  0.03449 -0.00661  0.98264  <------ this peak is close to the origin
    52.5  0.06905  0.02372  0.05632  <------ this one, too
    ...
 
so the strongest peak corresponds to the translation of molecules (0,0.5,0) but the origin peak is at 1/2 of that size, which appears significant.
 
 
=== Finally solving the structure ===
 
After thinking about the most likely way that James Holton used to produce the simulated data, I hypothesized that within each frame, the radiation damage is most likely constant, and that there is a jump in radiation damage from frame 1 to 2. Unfortunately for this scenario, the scaling algorithm in CORRECT and XSCALE was changed for the version of Dec-2010, such that it produces best results when the changes are smooth. Therefore, I tried the penultimate version (May-2010) of XSCALE - and indeed that gives significantly better results:
 
      NOTE:      Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION    NUMBER OF REFLECTIONS    COMPLETENESS R-FACTOR  R-FACTOR COMPARED I/SIGMA  R-meas  Rmrgd-F  Anomal  SigAno  Nano
  LIMIT    OBSERVED  UNIQUE  POSSIBLE    OF DATA  observed  expected                                      Corr
    8.05        1922    467      476      98.1%      4.0%      5.8%    1888  22.37    4.5%    2.5%    84%  1.952    142
    5.69        3494    864      882      98.0%      4.7%      6.0%    3429  20.85    5.4%    3.2%    77%  1.707    297
    4.65        4480    1111      1136      97.8%      5.1%      5.9%    4395  21.13    5.8%    3.3%    68%  1.518    406
    4.03        5197    1325      1357      97.6%      5.3%      6.0%    5101  20.57    6.1%    3.8%    48%  1.280    499
    3.60        5915    1500      1533      97.8%      6.0%      6.3%    5803  19.99    6.9%    4.1%    41%  1.169    572
    3.29        6601    1657      1694      97.8%      6.5%      6.5%    6476  19.42    7.5%    4.6%    27%  1.066    634
    3.04        7080    1789      1830      97.8%      7.6%      7.2%    6948  17.50    8.7%    5.4%    23%  1.037    693
    2.85        7682    1945      1979      98.3%      8.8%      9.0%    7528  14.75    10.1%    7.0%    15%  0.935    750
    2.68        8099    2062      2100      98.2%      11.0%    11.1%    7933  12.81    12.7%    9.1%    13%  0.881    795
    2.55        8351    2155      2201      97.9%      13.3%    13.7%    8178  11.16    15.4%    11.0%    12%  0.872    836
    2.43        9195    2327      2376      97.9%      16.5%    17.2%    9003    9.49    19.0%    15.1%    8%  0.838    904
    2.32        9495    2377      2428      97.9%      19.8%    20.3%    9304    8.62    22.7%    17.3%    4%  0.818    934
    2.23        9936    2498      2551      97.9%      20.8%    21.7%    9751    8.30    23.9%    17.5%    4%  0.830    987
    2.15      10217    2577      2622      98.3%      23.3%    24.0%    9990    7.74    26.7%    19.2%    4%  0.814    998
    2.08      10710    2704      2766      97.8%      27.1%    28.6%    10506    6.82    31.1%    23.5%    5%  0.812    1071
    2.01      10899    2777      2839      97.8%      28.1%    29.2%    10648    6.46    32.3%    25.0%    6%  0.813    1059
    1.95      11361    2878      2937      98.0%      34.4%    35.5%    11134    5.55    39.5%    30.3%    3%  0.780    1136
    1.90      11639    2941      3000      98.0%      40.5%    41.5%    11403    4.88    46.6%    35.9%    0%  0.787    1163
    1.85      12020    3068      3123      98.2%      52.2%    55.1%    11752    3.79    60.0%    47.4%    6%  0.775    1195
    1.80      11506    3003      3173      94.6%      60.8%    64.8%    11229    3.23    70.1%    58.8%    0%  0.765    1148
    total      165799  42025    43003      97.7%      11.7%    12.3%  162399  10.07    13.5%    14.8%    17%  0.908  16219
 
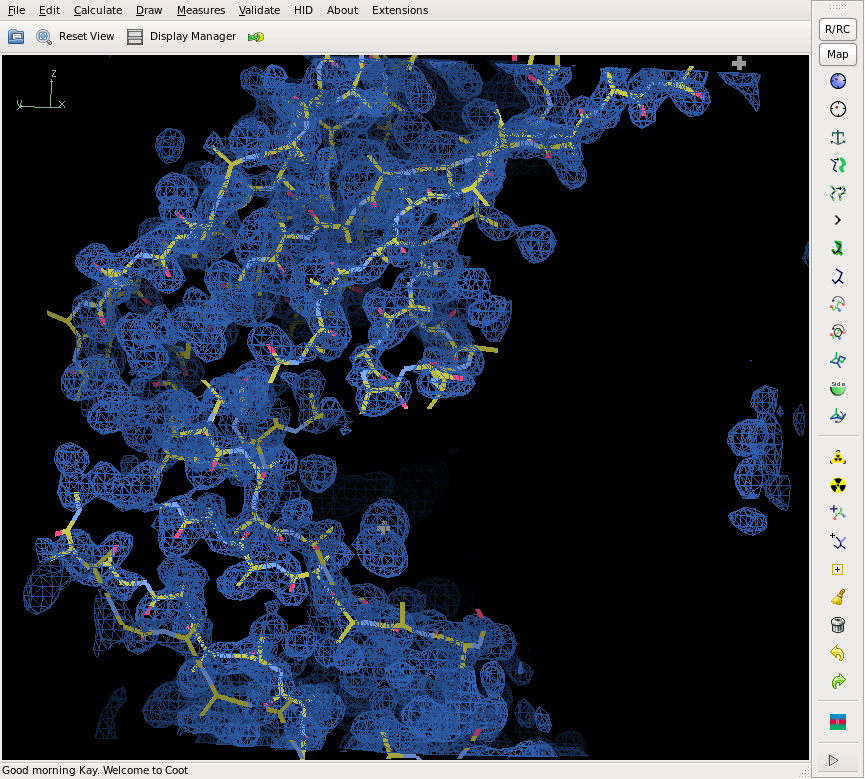
Using these data (stored in [https://{{SERVERNAME}}/pub/xds-datared/1g1c/xscale.oldversion]), I was finally able to solve the structure (see screenshot below) - SHELXE traced 160 out of 198 residues. All files produced by SHELXE are in [https://{{SERVERNAME}}/pub/xds-datared/1g1c/shelx].
 
[[File:1g1c-shelxe.png]]
 
It is worth mentioning that James Holton confirmed that my hypothesis is true; he also says that this approach is a good approximation for a multi-pass data collection.
 
However, generally (i.e. for real data) the smooth scaling (which also applies to absorption correction and detector modulation) gives better results than the previous method of assigning the same scale factor to all reflections of a frame; in particular, it correctly treats those reflections near the border of two frames. 
 
Phenix.refine against these data gives:
Start R-work = 0.3449, R-free = 0.3560
Final R-work = 0.2194, R-free = 0.2469
which is only 0.15%/0.10% better in R-work/R-free than the previous best result (see above).
 
This example shows that it is important to
* have the best data available if a structure is difficult to solve
* know the options (programs, algorithms)
* know as much as possible about the experiment
Retrieved from "https://wiki.uni-konstanz.de/xds/index.php/Special:MobileDiff/2362...4082"