3CSL: Difference between revisions
| Line 186: | Line 186: | ||
== Scaling == | == Scaling == | ||
This is XSCALE.INP - we don't try anything fancy: | |||
SPACE_GROUP_NUMBER= 22 | |||
UNIT_CELL_CONSTANTS= 156.80 163.12 595.87 90.000 90.000 90.000 | |||
OUTPUT_FILE=hr.ahkl | |||
INPUT_FILE=../xds.hr1/XDS_ASCII.HKL | |||
OUTPUT_FILE=pk.ahkl | |||
INPUT_FILE=../xds.pk/XDS_ASCII.HKL | |||
OUTPUT_FILE=ip.ahkl | |||
INPUT_FILE=../xds.ip/XDS_ASCII.HKL | |||
and this is an excerpt from XSCALE.LP: | |||
CORRELATIONS BETWEEN INPUT DATA SETS AFTER CORRECTIONS | |||
DATA SETS NUMBER OF COMMON CORRELATION RATIO OF COMMON B-FACTOR | |||
#i #j REFLECTIONS BETWEEN i,j INTENSITIES (i/j) BETWEEN i,j | |||
1 2 38920 0.986 1.0028 -0.1467 | |||
1 3 36555 0.985 0.9971 0.2041 | |||
2 3 35630 0.989 1.0038 -0.0116 | |||
These correlations are worse than what I like to see from MAD datasets. Some of the badness is maybe due to the fact that we used an unrealistic high-resolution limit. If we use INCLUDE_RESOLUTION_RANGE=50 3 the correlations are | |||
The file further reports CHI^2-VALUE OF FIT OF CORRECTION FACTORS around 1.15 which indicates that the scaling model is not entirely adequate, but it is unclear what to change, so we leave it at that (we could use STRICT_ABSORPTION_CORRECTION=TRUE to bring the number closer to 1). | |||
Then we learn | |||
****************************************************************************** | |||
CORRECTION PARAMETERS FOR THE STANDARD ERROR OF REFLECTION INTENSITIES | |||
****************************************************************************** | |||
The variance v0(I) of the intensity I obtained from counting statistics is | |||
replaced by v(I)=a*(v0(I)+b*I^2). The model parameters a, b are chosen to | |||
minimize the discrepancies between v(I) and the variance estimated from | |||
sample statistics of symmetry related reflections. This model implicates | |||
an asymptotic limit ISa=1/SQRT(a*b) for the highest I/Sigma(I) that the | |||
experimental setup can produce (Diederichs (2010) Acta Cryst D66, 733-740). | |||
Often the value of ISa is reduced from the initial value ISa0 due to systematic | |||
errors showing up by comparison with other data sets in the scaling procedure. | |||
(ISa=ISa0=-1 if v0 is unknown for a data set.) | |||
a b ISa ISa0 INPUT DATA SET | |||
6.329E+00 3.527E-04 21.17 22.36 ../xds.hr1/XDS_ASCII.HKL | |||
7.255E+00 8.432E-04 12.79 13.43 ../xds.pk/XDS_ASCII.HKL | |||
6.151E+00 6.548E-04 15.76 16.97 ../xds.ip/XDS_ASCII.HKL | |||
which says that the high-remote indeed scales best of the three datasets, and the peak the worst. This is the output for high-remote - not too impressing! | |||
****************************************************************************** | |||
STATISTICS OF SCALED OUTPUT DATA SET : hr.ahkl | |||
FILE TYPE: XDS_ASCII MERGE=FALSE FRIEDEL'S_LAW=FALSE | |||
450 OUT OF 419653 REFLECTIONS REJECTED | |||
419203 REFLECTIONS ON OUTPUT FILE | |||
****************************************************************************** | |||
... | |||
NOTE: Friedel pairs are treated as different reflections. | |||
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION | |||
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno | |||
Nano | |||
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr | |||
12.39 5724 2008 2112 95.1% 2.5% 3.2% 5674 30.03 3.2% 2.3% 67% 1.522 850 | |||
8.76 10864 3684 3837 96.0% 3.0% 3.5% 10807 26.32 3.7% 3.0% 62% 1.615 1649 | |||
7.15 13926 4749 4984 95.3% 4.3% 4.3% 13862 21.17 5.3% 5.0% 47% 1.397 2149 | |||
6.19 16773 5747 5895 97.5% 5.8% 5.6% 16708 16.66 7.1% 7.2% 30% 1.135 2664 | |||
5.54 19099 6546 6690 97.8% 6.8% 6.5% 19008 14.51 8.4% 9.1% 24% 1.078 3041 | |||
5.06 20933 7167 7374 97.2% 6.9% 6.7% 20828 14.04 8.6% 10.2% 17% 0.999 3321 | |||
4.68 22497 7721 7993 96.6% 6.5% 6.2% 22372 14.51 8.1% 9.9% 15% 0.957 3564 | |||
4.38 24415 8374 8666 96.6% 6.9% 6.6% 24280 13.74 8.5% 10.7% 12% 0.919 3870 | |||
4.13 26251 8985 9164 98.0% 8.7% 8.4% 26113 11.47 10.7% 13.9% 8% 0.863 4203 | |||
3.92 28037 9562 9686 98.7% 11.0% 10.8% 27878 9.38 13.5% 17.9% 6% 0.829 4485 | |||
3.74 29520 10119 10241 98.8% 13.3% 13.4% 29337 7.75 16.4% 22.1% 6% 0.813 4746 | |||
3.58 30822 10537 10662 98.8% 15.9% 15.9% 30639 6.74 19.6% 26.3% 8% 0.818 4933 | |||
3.44 32336 11005 11104 99.1% 21.2% 21.6% 32151 5.20 26.0% 35.8% 5% 0.786 5164 | |||
3.31 32608 11518 11593 99.4% 26.8% 27.5% 32195 4.07 33.1% 48.5% 3% 0.764 5248 | |||
3.20 27228 11396 11998 95.0% 33.2% 34.5% 25691 2.79 42.5% 66.2% 4% 0.729 4287 | |||
3.10 22192 10787 12431 86.8% 41.3% 43.7% 19573 1.94 54.3% 83.7% 1% 0.711 3403 | |||
3.00 18768 10018 12806 78.2% 53.3% 56.5% 15662 1.49 71.6% 110.8% -3% 0.669 2893 | |||
2.92 15878 9250 13096 70.6% 67.6% 71.8% 12570 1.09 93.3% 141.2% -1% 0.670 2408 | |||
2.84 13496 8654 13568 63.8% 74.1% 78.5% 9579 0.88 104.4% 158.4% 1% 0.662 1796 | |||
2.77 7836 6348 13844 45.9% 97.6% 103.5% 2966 0.58 137.9% 207.6% 1% 0.657 545 | |||
total 419203 164175 187744 87.4% 10.2% 10.4% 397893 7.99 12.8% 24.6% 14% 0.882 65219 | |||
== Structure solution == | == Structure solution == | ||
Revision as of 09:31, 19 March 2011
HasA/R (PDB id 3CSL) is a complex of a 22-stranded beta-barrel outer membrane protein (HAsR, 865 residues), its hemophore (HasA, 206 residues), and heme. The structure and its biological implications are described in "Heme uptake across the outer membrane as revealed by crystal structures of the receptor-hemophore complex" (Krieg, S., Huché, F., Diederichs, K., Izadi-Pruneyre, N., Lecroisey, A., Wandersman, C., Delepelaire, P., Welte, W. (2009), Proc. Nat. Acad. Sci. Vol. 106 pp. 1045-1050.)
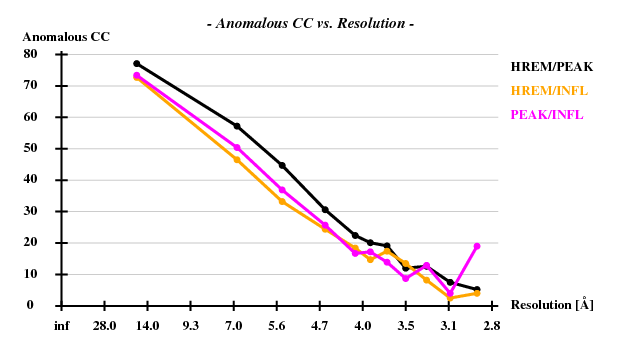
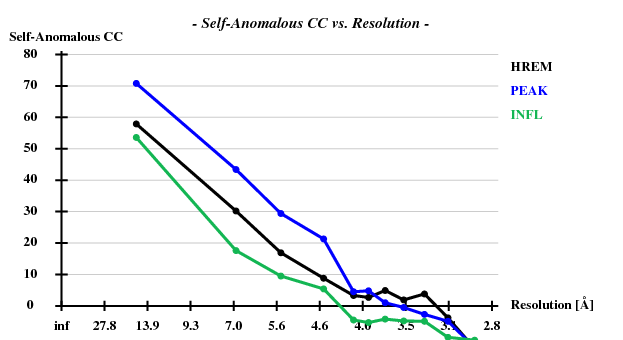
3-wl SeMet-MAD data were collected at beamline X06SA of the SLS in November 2006 on a MarCCD detector. HasA/R crystallizes in spacegroup F222; cell parameters are a=157Å, b=163Å, c=596Å. There are 2 complexes per ASU. Data to about 3.0Å could be collected from this crystal, but the anomalous data are useful to about 5Å only. The ordered part of HasR has residues 112-865 and harbours 9 SeMet residues. The ordered part of HasA has 173 residues, one of which is SeMet - but that is mostly disordered.
These MAD data, giving a structure with an average B of 100 Å2, constitute a project that is challenging for humans, and currently too difficult for automatic methods of structure solution and model building. The deposited 3CSL structure was not obtained from these MAD data alone, but the model was actually refined against slightly better (2.7Å) data collected on a native crystal at the ESRF.
XDS data reduction of high-remote, peak and inflection
The script generate_XDS.INP may be used to get a suitable first XDS.INP file for each of the three wavelengths. Unfortunately the beamline software did not put the correct X and Y position of the direct beam into the header. So you will have to find this yourself, using adxv or XDS-viewer. Or just use:
ORGX= 1536 ORGY= 1520
The other thing that you might want to try yourself, or just fill in, is
VALUE_RANGE_FOR_TRUSTED_DETECTOR_PIXELS=8000. 30000. ! often 8000 is ok
instead of the the default (7000. 30000.). This results in a good mask for the beamstop shadow.
It turns out that the spot shapes are actually so irregular that XDS stops after the IDXREF step, with a long warning message. This is because it cannot index (within default error margins) enough reflections (50% is the cutoff). When that occurs, one simply continues with the step after IDXREF:
JOBS= DEFPIX INTEGRATE CORRECT
Other than that, the three MAD wavelengths can be processed once with default parameters, as written into XDS.INP by generate_XDS.INP. This data reduction therefore proceeds in spacegroup P1, but the correct spacegroup (22) is identified by CORRECT.
Optimization: after this first data reduction pass, I use the "post-refined" geometric parameters, and the correct spacegroup (as given in CORRECT.LP, and written to GXPARM.XDS), for a second pass. Thus I need to
mv GXPAM.XDS XPARM.XDS
and modify XDS.INP to read
JOBS= INTEGRATE CORRECT
Afterwards, another xds_par run gives the final intensities. Repeating this optimization sometimes helps.
Peak
360 frames (0.5° oscillation) at the peak wavelength were collected after the high-remote data. They can be downloaded from here (1.9 Gb). This peak dataset is somewhat difficult to index; if the results are really bad (e.g. distance refining far away from 370 mm) with the default 180 frames, then just try with 90 or 270 frames.
This is an excerpt from CORRECT.LP :
REFINED PARAMETERS: DISTANCE BEAM ORIENTATION CELL AXIS
USING 166758 INDEXED SPOTS
STANDARD DEVIATION OF SPOT POSITION (PIXELS) 1.80
STANDARD DEVIATION OF SPINDLE POSITION (DEGREES) 0.61
CRYSTAL MOSAICITY (DEGREES) 0.557
DIRECT BEAM COORDINATES (REC. ANGSTROEM) 0.001590 -0.003616 1.021443
DETECTOR COORDINATES (PIXELS) OF DIRECT BEAM 1536.60 1519.03
DETECTOR ORIGIN (PIXELS) AT 1528.72 1536.95
CRYSTAL TO DETECTOR DISTANCE (mm) 370.85
LAB COORDINATES OF DETECTOR X-AXIS 1.000000 0.000000 0.000000
LAB COORDINATES OF DETECTOR Y-AXIS 0.000000 1.000000 0.000000
LAB COORDINATES OF ROTATION AXIS 0.999995 -0.001537 -0.002692
COORDINATES OF UNIT CELL A-AXIS -41.622 -128.332 80.636
COORDINATES OF UNIT CELL B-AXIS 45.889 72.744 139.459
COORDINATES OF UNIT CELL C-AXIS -551.193 220.474 66.370
REC. CELL PARAMETERS 0.006362 0.006103 0.001674 90.000 90.000 90.000
UNIT CELL PARAMETERS 157.174 163.848 597.351 90.000 90.000 90.000
E.S.D. OF CELL PARAMETERS 7.9E-01 8.7E-01 3.0E+00 0.0E+00 0.0E+00 0.0E+00
SPACE GROUP NUMBER 22
...
a b ISa
7.764E+00 7.144E-04 13.43
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.29 26331 7014 7090 98.9% 5.3% 5.5% 26314 20.22 6.3% 4.2% 71% 1.936 3195
5.90 48060 12542 12555 99.9% 8.4% 8.4% 48060 13.36 9.8% 8.5% 45% 1.322 5963
4.83 61534 16074 16144 99.6% 11.0% 10.6% 61534 10.69 12.9% 13.2% 27% 1.051 7728
4.19 71665 18994 19085 99.5% 12.5% 11.8% 71658 9.61 14.6% 16.0% 18% 0.920 9190
3.75 77668 21598 21677 99.6% 19.5% 19.3% 77668 6.33 23.0% 27.1% 6% 0.794 10491
3.42 78594 23767 23865 99.6% 28.3% 29.5% 78582 4.14 34.0% 45.0% 4% 0.735 11548
3.17 64135 24351 26036 93.5% 42.7% 46.4% 60830 2.18 52.9% 78.5% 2% 0.689 9568
2.97 40861 20207 27920 72.4% 63.8% 72.3% 35172 1.18 83.3% 118.6% 1% 0.657 6055
2.80 23238 15074 29715 50.7% 89.5% 104.9% 15359 0.63 122.8% 175.5% 5% 0.646 2502
total 492086 159621 184087 86.7% 14.8% 15.1% 475177 6.17 17.8% 30.6% 22% 0.901 66240
NUMBER OF REFLECTIONS IN SELECTED SUBSET OF IMAGES 501334
NUMBER OF REJECTED MISFITS 8429
NUMBER OF SYSTEMATIC ABSENT REFLECTIONS 0
NUMBER OF ACCEPTED OBSERVATIONS 492905
NUMBER OF UNIQUE ACCEPTED REFLECTIONS 159845
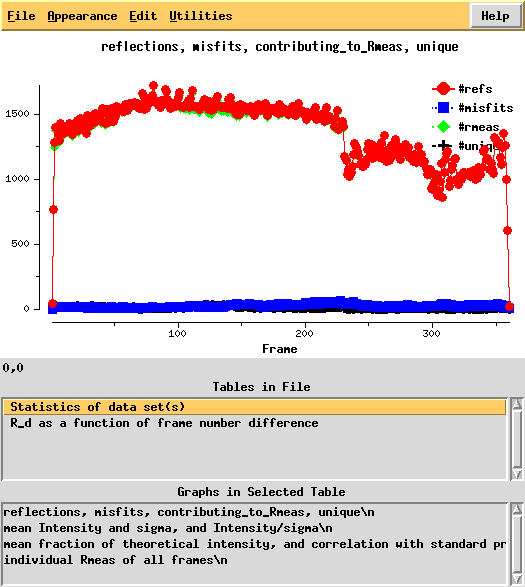
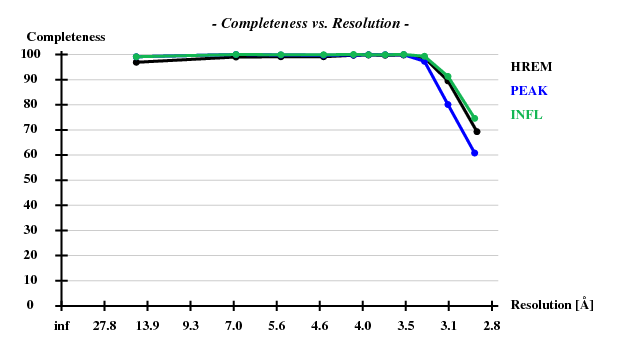
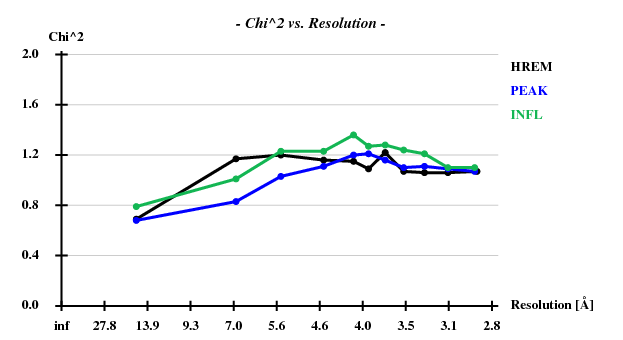
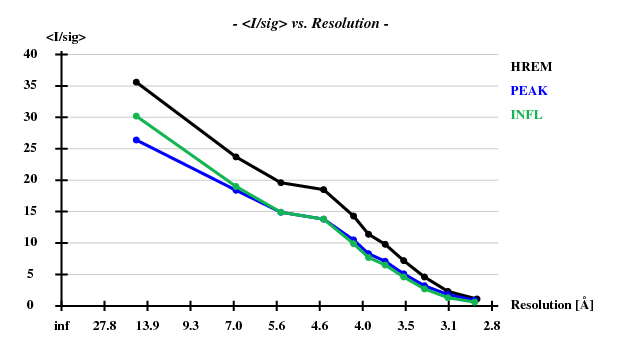
The verdict is clear: high mosaicity (> 0.5°) bad ISa, anomalous correlation > 30% only to about 5 A. The reason becomes clear if we load FRAME.cbf into XDS-Viewer, and zoom in:
It is clear that these split reflections provide bad data. Fortunately it seems that in other areas of the detector, the reflections look better.
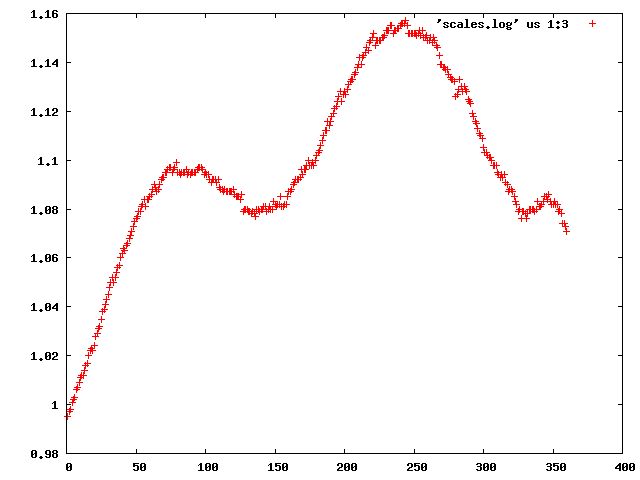
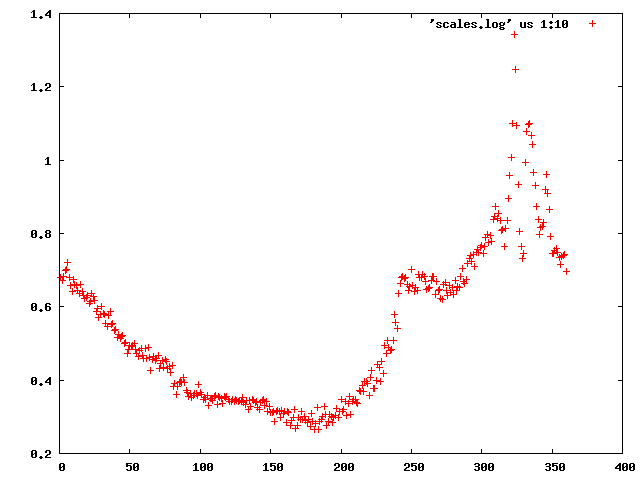
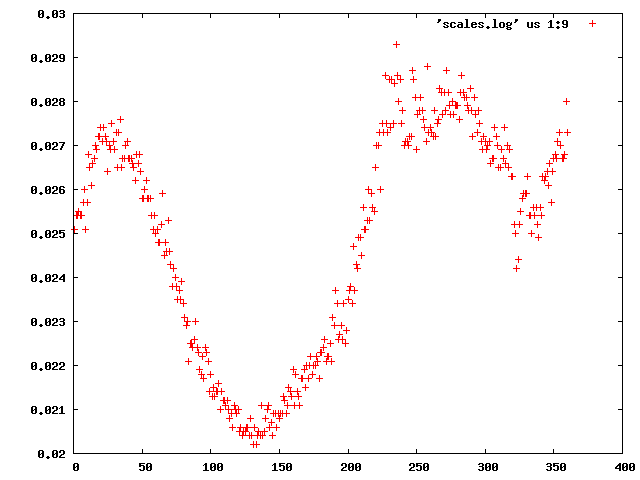
We can use the "scalefactors" jiffy to investigate the scale factor, and the estimates for mosaicity and beam divergence of each frame:
Next, we can use xdsstat to get frame-wise statistics from XDS_ASCII.HKL:
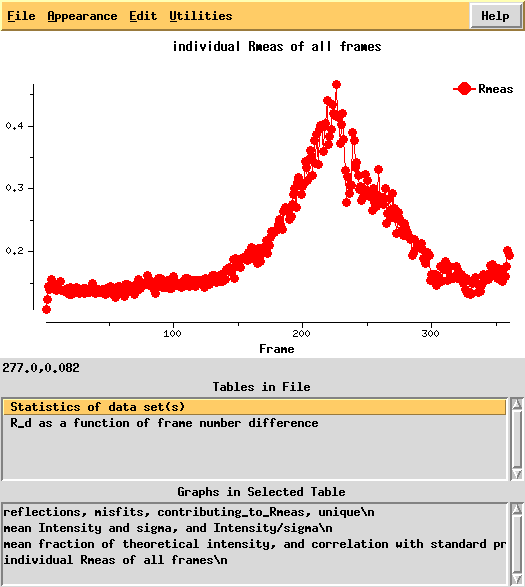
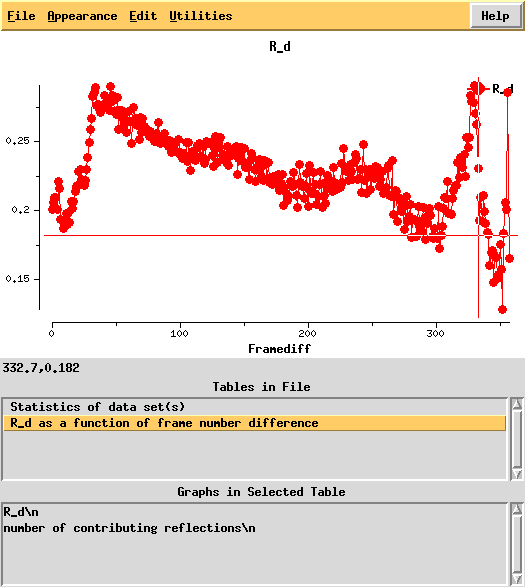
This shows a "jump" around frame 225 which is always bad for experimental phasing!
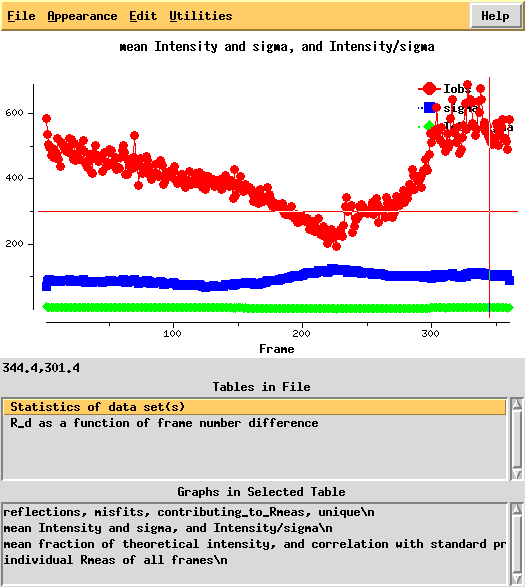
Around frame 225 the data are weakest, but they recover.
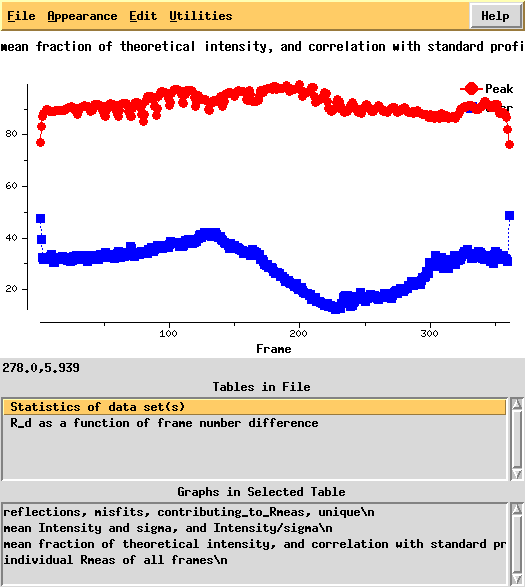
In particular the correlation against standard profiles (blue curve) is really low.
R-factors peak around frame 225.
R_d helps to quantify radiation damage. Unfortunately, for this dataset this "R-factor as a function of frame number difference" behaves wildly, so we cannot use 0-dose extrapolation, like we successfully did for 1Y13.
High-remote
Due to a beamline problem, high-remote data collection stopped after 269 frames of 0.5° (the final frame is already affected). After restart of the beamline, another 100 frames were collected but they later turned out to merge badly with the first 269 frames - a hint that the monochromator was still heating up, or similar. So the latter frames were left out. The 269 frames are here (1.4 Gb).
From CORRECT.LP :
a b ISa
6.595E+00 3.032E-04 22.36
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.21 20187 6913 7245 95.4% 2.9% 3.3% 20065 27.89 3.6% 2.9% 63% 1.625 3050
5.84 36272 12417 12782 97.1% 5.5% 5.3% 36116 17.46 6.8% 7.0% 33% 1.196 5727
4.78 46716 16015 16500 97.1% 6.8% 6.5% 46473 14.43 8.4% 10.0% 19% 1.004 7416
4.15 55299 18949 19484 97.3% 7.5% 7.2% 55003 13.00 9.3% 11.7% 10% 0.896 8818
3.71 63751 21798 22065 98.8% 12.2% 12.2% 63371 8.51 15.1% 20.2% 6% 0.819 10225
3.39 70787 24180 24422 99.0% 19.5% 20.0% 70378 5.58 24.0% 33.3% 5% 0.786 11343
3.14 61197 25100 26452 94.9% 32.5% 34.2% 57925 2.88 41.3% 63.9% 4% 0.740 9652
2.94 40481 21869 28566 76.6% 53.5% 57.8% 33568 1.42 72.1% 112.8% -2% 0.663 6208
2.77 24584 16962 30228 56.1% 76.4% 82.4% 15055 0.77 107.5% 163.0% 2% 0.660 2828
total 419274 164203 187744 87.5% 10.3% 10.4% 397954 8.06 12.9% 24.7% 14% 0.882 65267
NUMBER OF REFLECTIONS IN SELECTED SUBSET OF IMAGES 428770
NUMBER OF REJECTED MISFITS 9102
NUMBER OF SYSTEMATIC ABSENT REFLECTIONS 0
NUMBER OF ACCEPTED OBSERVATIONS 419668
NUMBER OF UNIQUE ACCEPTED REFLECTIONS 164343
Inflection
360 frames (0.5° oscillation) at the inflection wavelength were collected after the peak data. They can be downloaded from here (1.8 Gb).
CORRECT.LP has:
a b ISa
6.514E+00 5.329E-04 16.97
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
8.28 26530 7039 7111 99.0% 4.4% 4.6% 26516 23.79 5.2% 3.7% 57% 1.526 3211
5.90 48700 12589 12598 99.9% 8.7% 8.5% 48700 14.00 10.2% 9.2% 23% 1.052 5989
4.83 62546 16177 16208 99.8% 12.0% 11.5% 62546 10.85 13.9% 14.5% 12% 0.912 7784
4.18 72644 19076 19117 99.8% 13.6% 13.1% 72637 9.64 15.9% 17.3% 8% 0.850 9229
3.75 80829 21710 21740 99.9% 23.8% 24.0% 80829 5.92 27.9% 32.0% 1% 0.770 10553
3.42 86652 23874 23917 99.8% 38.5% 39.9% 86652 3.71 45.2% 53.8% 3% 0.737 11620
3.17 73630 25264 26115 96.7% 64.4% 68.0% 71837 1.82 78.5% 109.4% 3% 0.693 10945
2.96 48079 22582 28004 80.6% 99.2% 107.3% 43325 0.86 129.6% 186.7% 3% 0.654 7797
2.80 28417 17801 29828 59.7% 155.6% 168.5% 20099 0.43 214.2% 307.3% 3% 0.613 3713
total 528027 166112 184638 90.0% 17.6% 17.8% 513141 5.98 20.9% 38.7% 10% 0.816 70841
NUMBER OF REFLECTIONS IN SELECTED SUBSET OF IMAGES 534898
NUMBER OF REJECTED MISFITS 6486
NUMBER OF SYSTEMATIC ABSENT REFLECTIONS 0
NUMBER OF ACCEPTED OBSERVATIONS 528412
NUMBER OF UNIQUE ACCEPTED REFLECTIONS 166224
Scaling
This is XSCALE.INP - we don't try anything fancy:
SPACE_GROUP_NUMBER= 22 UNIT_CELL_CONSTANTS= 156.80 163.12 595.87 90.000 90.000 90.000 OUTPUT_FILE=hr.ahkl INPUT_FILE=../xds.hr1/XDS_ASCII.HKL OUTPUT_FILE=pk.ahkl INPUT_FILE=../xds.pk/XDS_ASCII.HKL OUTPUT_FILE=ip.ahkl INPUT_FILE=../xds.ip/XDS_ASCII.HKL
and this is an excerpt from XSCALE.LP:
CORRELATIONS BETWEEN INPUT DATA SETS AFTER CORRECTIONS DATA SETS NUMBER OF COMMON CORRELATION RATIO OF COMMON B-FACTOR #i #j REFLECTIONS BETWEEN i,j INTENSITIES (i/j) BETWEEN i,j 1 2 38920 0.986 1.0028 -0.1467 1 3 36555 0.985 0.9971 0.2041 2 3 35630 0.989 1.0038 -0.0116
These correlations are worse than what I like to see from MAD datasets. Some of the badness is maybe due to the fact that we used an unrealistic high-resolution limit. If we use INCLUDE_RESOLUTION_RANGE=50 3 the correlations are The file further reports CHI^2-VALUE OF FIT OF CORRECTION FACTORS around 1.15 which indicates that the scaling model is not entirely adequate, but it is unclear what to change, so we leave it at that (we could use STRICT_ABSORPTION_CORRECTION=TRUE to bring the number closer to 1).
Then we learn
******************************************************************************
CORRECTION PARAMETERS FOR THE STANDARD ERROR OF REFLECTION INTENSITIES
******************************************************************************
The variance v0(I) of the intensity I obtained from counting statistics is
replaced by v(I)=a*(v0(I)+b*I^2). The model parameters a, b are chosen to
minimize the discrepancies between v(I) and the variance estimated from
sample statistics of symmetry related reflections. This model implicates
an asymptotic limit ISa=1/SQRT(a*b) for the highest I/Sigma(I) that the
experimental setup can produce (Diederichs (2010) Acta Cryst D66, 733-740).
Often the value of ISa is reduced from the initial value ISa0 due to systematic
errors showing up by comparison with other data sets in the scaling procedure.
(ISa=ISa0=-1 if v0 is unknown for a data set.)
a b ISa ISa0 INPUT DATA SET
6.329E+00 3.527E-04 21.17 22.36 ../xds.hr1/XDS_ASCII.HKL
7.255E+00 8.432E-04 12.79 13.43 ../xds.pk/XDS_ASCII.HKL
6.151E+00 6.548E-04 15.76 16.97 ../xds.ip/XDS_ASCII.HKL
which says that the high-remote indeed scales best of the three datasets, and the peak the worst. This is the output for high-remote - not too impressing!
****************************************************************************** STATISTICS OF SCALED OUTPUT DATA SET : hr.ahkl FILE TYPE: XDS_ASCII MERGE=FALSE FRIEDEL'S_LAW=FALSE
450 OUT OF 419653 REFLECTIONS REJECTED 419203 REFLECTIONS ON OUTPUT FILE
******************************************************************************
...
NOTE: Friedel pairs are treated as different reflections.
SUBSET OF INTENSITY DATA WITH SIGNAL/NOISE >= -3.0 AS FUNCTION OF RESOLUTION
RESOLUTION NUMBER OF REFLECTIONS COMPLETENESS R-FACTOR R-FACTOR COMPARED I/SIGMA R-meas Rmrgd-F Anomal SigAno
Nano
LIMIT OBSERVED UNIQUE POSSIBLE OF DATA observed expected Corr
12.39 5724 2008 2112 95.1% 2.5% 3.2% 5674 30.03 3.2% 2.3% 67% 1.522 850
8.76 10864 3684 3837 96.0% 3.0% 3.5% 10807 26.32 3.7% 3.0% 62% 1.615 1649
7.15 13926 4749 4984 95.3% 4.3% 4.3% 13862 21.17 5.3% 5.0% 47% 1.397 2149
6.19 16773 5747 5895 97.5% 5.8% 5.6% 16708 16.66 7.1% 7.2% 30% 1.135 2664
5.54 19099 6546 6690 97.8% 6.8% 6.5% 19008 14.51 8.4% 9.1% 24% 1.078 3041
5.06 20933 7167 7374 97.2% 6.9% 6.7% 20828 14.04 8.6% 10.2% 17% 0.999 3321
4.68 22497 7721 7993 96.6% 6.5% 6.2% 22372 14.51 8.1% 9.9% 15% 0.957 3564
4.38 24415 8374 8666 96.6% 6.9% 6.6% 24280 13.74 8.5% 10.7% 12% 0.919 3870
4.13 26251 8985 9164 98.0% 8.7% 8.4% 26113 11.47 10.7% 13.9% 8% 0.863 4203
3.92 28037 9562 9686 98.7% 11.0% 10.8% 27878 9.38 13.5% 17.9% 6% 0.829 4485
3.74 29520 10119 10241 98.8% 13.3% 13.4% 29337 7.75 16.4% 22.1% 6% 0.813 4746
3.58 30822 10537 10662 98.8% 15.9% 15.9% 30639 6.74 19.6% 26.3% 8% 0.818 4933
3.44 32336 11005 11104 99.1% 21.2% 21.6% 32151 5.20 26.0% 35.8% 5% 0.786 5164
3.31 32608 11518 11593 99.4% 26.8% 27.5% 32195 4.07 33.1% 48.5% 3% 0.764 5248
3.20 27228 11396 11998 95.0% 33.2% 34.5% 25691 2.79 42.5% 66.2% 4% 0.729 4287
3.10 22192 10787 12431 86.8% 41.3% 43.7% 19573 1.94 54.3% 83.7% 1% 0.711 3403
3.00 18768 10018 12806 78.2% 53.3% 56.5% 15662 1.49 71.6% 110.8% -3% 0.669 2893
2.92 15878 9250 13096 70.6% 67.6% 71.8% 12570 1.09 93.3% 141.2% -1% 0.670 2408
2.84 13496 8654 13568 63.8% 74.1% 78.5% 9579 0.88 104.4% 158.4% 1% 0.662 1796
2.77 7836 6348 13844 45.9% 97.6% 103.5% 2966 0.58 137.9% 207.6% 1% 0.657 545
total 419203 164175 187744 87.4% 10.2% 10.4% 397893 7.99 12.8% 24.6% 14% 0.882 65219
Structure solution
We use hkl2map for solving the structure.
SHELXC statistics
SHELXD statistics
SHELXE statistics
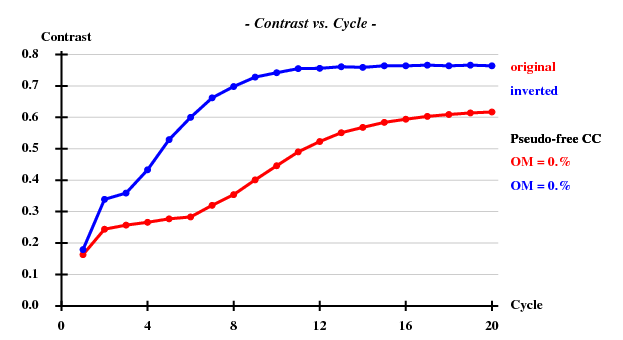
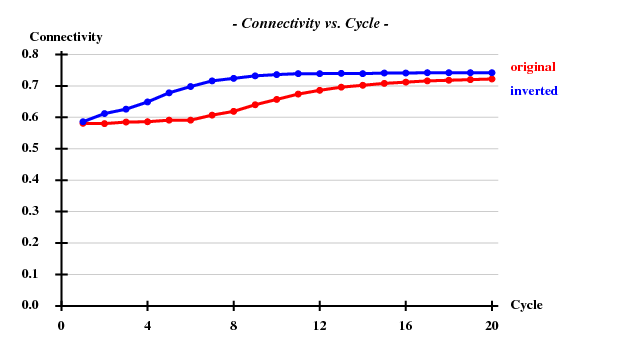
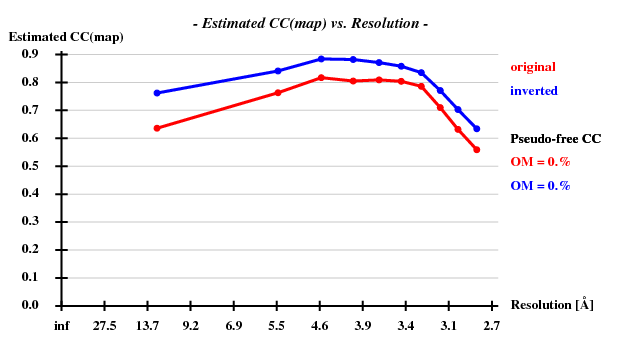
Since there are 1852 residues in the ASU, the solvent content is about 72.5%. The correct hand ("inverted") becomes immediately clear - it is superior in all respects than the "original" hand.
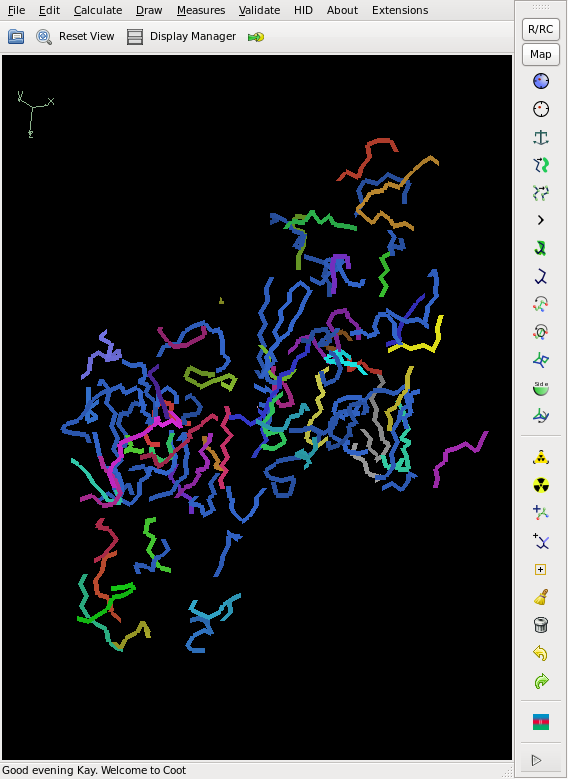
Then we try to get a poly-ala backbone tracing, using the 16 Se sites found by SHELXD:
shelxe.beta -a -q -m15 -s0.725 -b -h16 -n2 -i mad mad_fa
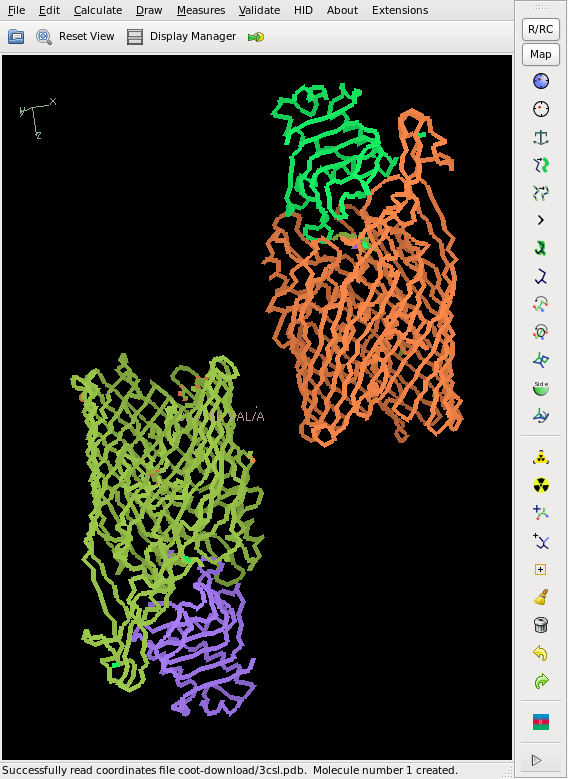
This does not yield a complete chain, but rather about 50% of it, and the CC is slightly less than 20%, so that we cannot consider the structure as solved yet. However, the phases are good enough for finding 2 additional sites. We iterate this, and finally the Se sites all have a density of at least 20 sigma. The model from shelxe as well as the deposited structure are shown below:
No doubt that one can solve the structure from here, maybe after HA refinement with SHARP, and model building with buccanneer or Arp/wArp.
Availability of data
There are files with amplitudes (3csl-pk-F.mtz, 3csl-rh-F.mtz, 3csl-ip-F.mtz) and intensities (3csl-pk-I.mtz, 3csl-rh-I.mtz, 3csl-ip-I.mtz) as well as mad_i.pdb and mad_i.phs (written by SHELXE) available from [1].
additional information for those who want to complete the structure
These are the entire sequences of HasR and HasA - before solving the structure it was not known that the N-terminus of HasR was disordered.
AQAEASSAQAAQQKNFNIAAQPLQSAMLRFAEQAGMQVFFDEVKLDGMQAAALNGSMSVEQGLRRLIGGNPVAFRLQPQGQIVLSRLPTANGDGGALALD SLTVLGAGGNNANDWVYDEPRSVSVISREQMDNRPARHAADILEQTTGAYSSVSQQDPALSVNIRGIQDYGRVNMNIDGMRQNFQKSGHGQRNGTMYIDS ELLSGVTIDKGTTGGMGSAGTLGGIATFNTVSASDFLAPGKELGGKLHASTGDNGTHFIGSGILALGNETGDILLAASERHLGDYWPGNKGDIGNIRINN DTGNYDRYAESIKNNKIPDTHYRMHSRLAKVGWNLPANQRLQLSYLQTQTASPIAGTLTNLGTRPPYELGWKRTGYTDVMARNAAFDYSLAPEDVDWLDF QAKLYYVDTQDDSDTYSTSSLLDNGYATRTRLRTYGAQAQNTSRFSLAPGHDFRANYGLEFYYDKATSDSSRQGMEGVTPAGNRSVASLFANLTYDYDGW LTLEGGLRYDRYRLRGQTGLSYPDLAKDGQRYTIDNPCKALRLTGCSTTTREDWDVDRDQGKLSPTLAVAVRPGVEWLELYTTYGKSWRPPAITETLTNG SAHSSSTQYPNPFLQPERSRAWEVGFNVQQPDLWFEGDRLVAKVaYFDTKVDNYINLAIDRNKPGLVQPSIGNAAYVNNLSKTRFRGLEYQLNYDAGVFY ADLTYTHMIGKNEFCSNKAWLGGRLRYGDGSRRGNFYVEPDAASNDFVTCDGGTQFGSAAYLPGDRGSVTLGGRAFDRKLDAGVTVRFAPGYQDSSVPSN YPYLADWPKYTLFDLYASYKLTDSLTLRGSVENLTNRAYVVSYGETLANTLGRGRTVQGGVEYRF MRGSHHHHHHGIRMRARYPAFSVNYDSSFGGYSIHDYLGQWASTFGDVNH TNGNVTDANSGGFYGGSLSGSQYAISSTANQVTAFVAGGNLTYTLFNEPA HTLYGQLDSLSFGDGLSGGDTSPYSIQVPDVSFGGLNLSSLQAQGHDGVV HQVVYGLMSGDTGALETALNGILDDYGLSVNSTFDQVAAATAVGVQHADS PELLAA